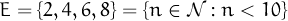
(Enllaç a aquest document en html)
(Enllaç a la versió pdf d’aquest document)
(Enllaç a la font LaTeX)
(Enllaç als fitxers de les figures)
(Enllaç al fitxer de definicions latex)
Aquest document inclou una proposta completa del que podria ser una nova primera setmana dedicada a una petita introducció al llenguatge formal de les matemàtiques i una possible segona setmana per a mates II o III.
La secció T0 correspondria a una primera setmana de mates I, la secció T0B a la possible segona setmana. Inclouen propostes de guies estructurades en slides, qüestionaris breus pre-classe per després de la primera lectura de la guia i llistes d’exercicis.
Es tracta de fer una lleu introducció al llenguatge formal, limitat a l’àlgebra de conjunts i la de Boole elemental. Posem davant els conjunts perquè probablement els són més familiars i els poden ajudar a entrar en el més abstracta de la lògica formal, que tractem només somerament, sense entrar en taules de veritat, demostracions, etc. que poden ser objecte de tractament a mates II o III.
Referències:
Un conjunt és una col·lecció d’objectes considerada com una sola entitat.
Dels objectes en diem que són els membres o elements del conjunt.
Exemples:
Els conjunts es poden descriure per enumeració o a través d’una propietat que els seus elements o membres han de satisfer. El darrer exemple el podem descriure:
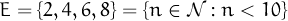
El signe ∈ es llegeix “pertany a” i l’usem per afirmar que un element forma part d’un conjunt. Si no en forma part, escriurem
a A.
____________________________________________________________________________________________
A.
____________________________________________________________________________________________
Diem que un conjunt A és subconjunt d’un conjunt B si tots els elements de A també ho són de B. Llavors escribim A ⊂ B.
Per exemple, si A és el conjunt dels treballadors d’una empresa i B és el conjunt dels administratius de l’empresa, B ⊂ A.
Sempre es compleix que A ⊂ A. De fet, dos conjunts A i B són iguals, A = B si i només si A ⊂ B i B ⊂ A.
El conjunt especial ∅és el que no té cap element, per exemple. el conjunt de les vaques que poden volar._______________
| Unió de A i B | A ∪ B | Els elements que pertanyen almenys a un dels dos |
| Intersecció | A ∩ B | Els elements que pertanyen a tots dos |
| Diferència | A\B | Elements de A que no ho són de B |
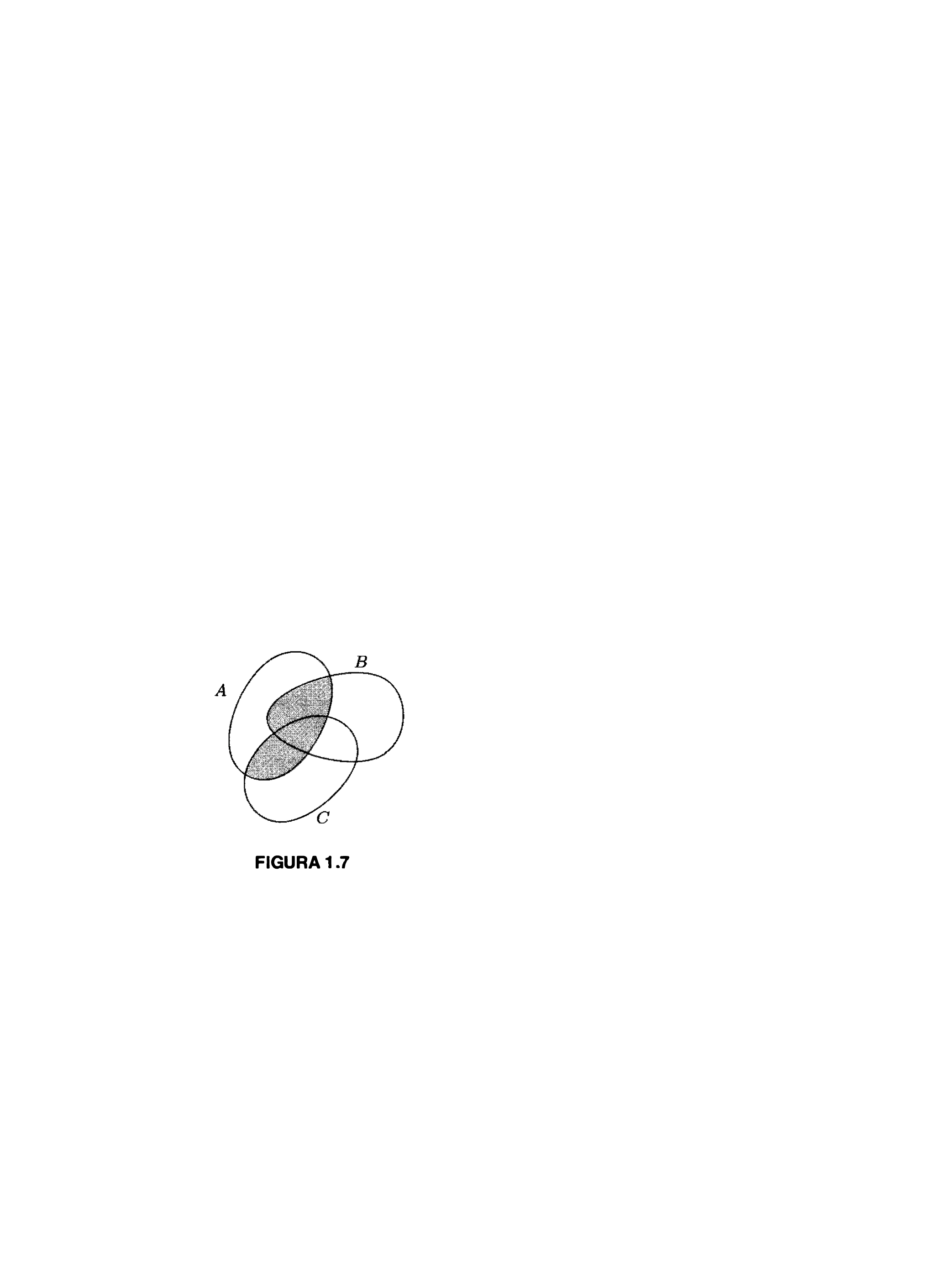
Els diagrames de Venn són útils per visualitzar això.

Exemple: Si A = {a,b,c,d} i B = {c,d,e,f,g}, llavors
Es compleixen les següents propietats, que podem comprovar amb els corresponents diagrames de Venn:
En el cas que tractem amb conjunts inclosos en un cert univers, podem parlar del conjunt complementari, el que està format pels elements que no hi pertanyen. Indiquem amb A′ o Ac el complementari de A.
Es compleixen les següents propietats, que podem comprovar amb els corresponents diagrames de Venn:
Podeu practicar amb diagrames de Venn de conjunts i els seus complementaris a https://www.geogebra.org/m/KSuUb2TR.
Per exemple, així es veu (A ∪ B)′: 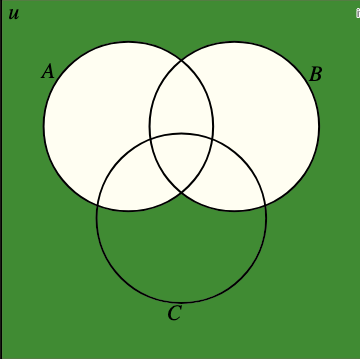 _____________________________________________________________________________________________________
_____________________________________________________________________________________________________
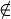 {a,b,c,d}
{a,b,c,d}
 correspon a
correspon a
Una proposició o enunciat és una afirmació que pot ser veritable o falsa. Per exemple “2 + 2 = 5”, o “x = 2 és solució de x2 - 4”.
No considerem que “El color vermell és bonic” sigui una proposició.
Sovint expressem una proposició amb una lletra, per exemple p = “5 és un nombre primer”. ____________________
| És veritat quan | ||
| Negació de p | ¬p | p és falsa |
| Disjunció de p i q | p ó q, p ∨ q | Almenys una de les dues és veritat |
| Conjunció de p i q | p i q, p ∧ q | Totes dues són veritat |
| Implicació | p ⇒ q | Sempre que p és veritat, q també ho és |
| Equivalència | p ⇔ q | Sempre que una de les dues és veritat, l’altra també |
Exemples:
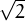
Quan tenim p ⇒ q, diem que:
Exemples:
Per a p,q proposicions,
Exemples:
Observem el paral·lelisme entre:
| Negació i complementari d’un conjunt: | x ∈ A′ equival a ¬(x ∈ A). |
| Disjunció i unió de conjunts: | x ∈ A ∪ B equival a x ∈ A ∨ x ∈ B. |
| Conjunció i intersecció: | x ∈ A ∩ B equival a x ∈ A ∧ x ∈ B. |
| Implicació i inclusió: | A ⊂ B equival a x ∈ A ⇒ x ∈ B. |
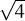 x = 2
x = 2
Més clickers sobre logica proposicional bàsica: http://myslu.stlawu.edu/~plock/Math280Clicker/Ma280-1.ppt
A la mateixa pàgina n’hi ha d’altres sobre quantificadors, http://myslu.stlawu.edu/~plock/Math280Clicker/Ma280-3.ppt, demostracions, etc que podrien ser utils per una setmana de mates II.

Es tracta d’ampliar una mica el que s’ha fet a Matemàtiques I sobre el llenguatge. Allà s’ha tractat el llenguatge dels conjunts i els elements bàsics de la lògica booleana.
Aquí introduirem els quantificadors universal i existencial amb un repàs de les regles bàsiques dels connectors i en una segona guia alguns elements dels mètodes de demostració.
Referències:
Recordem:
| És veritat quan | ||
| Negació de p | ¬p | p és falsa |
| Disjunció de p i q | p ó q, p ∨ q | Almenys una de les dues és veritat |
| Conjunció de p i q | p i q, p ∧ q | Totes dues són veritat |
| Implicació | p ⇒ q | Sempre que p és veritat, q també ho és |
| Equivalència | p ⇔ q | Sempre que una de les dues és veritat, l’altra també |
I recordem encara:
| L1 | ¬(¬p) és equivalent a p |
| L2 | ¬(p ∧ q) és equivalent a ¬p ∨ ¬q |
| L3 | ¬(p ∨ q) és equivalent a ¬p ∧ ¬q |
| L4 | p ⇒ q és equivalent a ¬q ⇒ ¬p |
Nota: En llenguatge no formal hi ha expressions que poden confondre. Per exemple, en català, les expressions “Res no és gratuït, tot té un preu” i “Res és gratuït, tot té un preu” es consideren vàlides i equivalents. __________________
Si tenim un conjunt X i una afirmació p(x) sobre els seus elements x ∈ X que pot ser veritat o falsa, podem dir
| Escrivim | Llegim |
| ∀x ∈ X,p(x) | Per a tots els x de X, p(x) es compleix |
| ∃x ∈ X : p(x) | Existeix algún (almenys un) x de X tal que p(x) es compleix |
Exemples, per 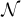 , el conjunt dels nombres naturals, les següents són veritat:
, el conjunt dels nombres naturals, les següents són veritat:
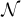 ,(n + 1)2 = n2 + 2n + 1
,(n + 1)2 = n2 + 2n + 1
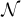 : n2 = 16
: n2 = 16
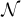 : n > 16
: n > 16
però les següents són falses:
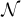 ,(n + 1)2 = n2 + 1
,(n + 1)2 = n2 + 1
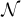 : n2 = 20
: n2 = 20
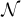 : n > n - 1
: n > n - 1
La negació canvia un quantificador en l’altre.
| El contrari de | Tot x compleix p(x) | és | Algun x no compleix p(x) |
| El contrari de | Algun x compleix p(x) | és | Tot x no compleix p(x) |
En versió formal:
¬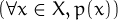 | equival a | ∃x ∈ X,¬p(x) |
¬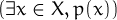 | equival a | ∀x ∈ X,¬p(x) |
Exemples:
Exemples en notació formal:
 ,n2 > n és ∃n ∈
,n2 > n és ∃n ∈ : n2 ≤ n
: n2 ≤ n
 : n2 < n + 25 és ∀n ∈
: n2 < n + 25 és ∀n ∈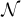 ,n2 ≤ n + 25
,n2 ≤ n + 25
Exemples (al tanto amb el llenguatge poc formal, pot induir a confusions, sovint va bé formalitzar la proposició)
Observa que si en una proposició es combina algun quantificador amb altres connectives, cal anar al tanto! I si a més a més s’hi barreja el llenguatge no formal, més perill!
Exemples
Formalitzem aquest darrer exemple: posem A el conjunt de països africans. p(a) = el país a te la Pfizer. q(a) = el país a té la Moderna”. Llavors traduïm:
Si recordem que ¬(p ⇒ q) és equivalent a p ∧ ¬q, podem dir ara:
| El contrari de | Per tot x es compleix p(x) ⇒ q(x) | és | Per algun x es té p(x) i ¬q(x) |
En aquesta guia introduïm les idees bàsiques dels mètodes de demostració matemàtica. Tractarem
La demostració per inducció quedaria per a treball opcional per a matrícula. ________________________________
És un mètode que consisteix en demostrar que una conclusió és veritat a partir de una o diverses hipòtesis veritables.
Exemple: Demostrar que la suma de dos nombres parells és un nombre parell.
La hipòtesi és que dos nombres n,m són parells.
La conclusió és que la suma n + m és parell.
Demostració: Suposant que n,m són nombres naturals parells, hem de demostrar que n + m és un nombre
parell. QED
Segons la definició de nombre parell, podem escriure n = 2k1,m = 2k2.
Llavors, n + m = 2k1 + 2k2 = 2(k1 + k2), i per tant, n + m és parell.
La que acabem de veure és una demostració directa: a partir de la hipòtesi fem una cadena de raonaments lògics correctes per arribar a la conclusió.
Un altre exemple: Demostrar que el quadrat d’un nombre parell és parell.
Demostració: Suposant que n és un nombre natural parell (hipòtesi), QED
hem de demostrar que n2 és un nombre parell (conclusió).
Segons la definició de nombre parell, podem escriure n = 2k.
Llavors, n2 = 4k2 = 2(2k2), i per tant, n2 és parell.
Proveu ara de demostrar que “El producte de dos nombres senars és senar”. _________________________________
Recordem que P ⇒ Q és equivalent a ¬Q ⇒ ¬P, o dit d’altra manera: Si P llavors Q és equivalent a “Si noQ, llavors noP”.
La demostració per contraposició de “Si P, llavors Q” consisteix en demostrar que “Si noQ, llavors noP”.
Exemple: Per demostrar que “Si n2 és parell, n és parell”, ho fem per contraposició, demostrarem que “Si n no és parell, n2 no és parell.”
Demostració: Si n és un nombre natural no parell, llavors és senar. QED
Si n és senar, com que el producte de dos senars és senar, n ⋅ n = n2 és senar.
La demostració per contradicció o per reducció a l’absurd consisteix en suposar falsa la conclusió i arribar a una contradicció, a una afirmació impossible de ser certa.
Exemple
Demostrar que 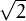 no és racional, és a dir que no es pot expressar com
no és racional, és a dir que no es pot expressar com 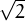 = a∕b amb a,b enters.
= a∕b amb a,b enters.
Demostració: Suposem contràriament que sí es pot tenir QED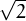 = a∕b amb a,b enters.
= a∕b amb a,b enters.
Si ambdós a i b són parells, els dividim per dos fins que no siguin tots dos parells.
Llavors tenim 2 = a2∕b2 o bé a2 = 2b2 i veiem que a2 és parell i per tant a és parell.
Podem escriure, a = 2k per algún enter k, a2 = 4k2 = 2b2, i tenim b2 = 2k2.
Resulta que b2 és parell i per tant b és parell també: contradicció perqué haviem vist que b
era senar!
Un exemple no matemàtic: El Sr. X no és culpable de l’assessinat de Y. QED
Demostració: Demostració per reducció a l’absurd:
Si contràriament fos culpable, necessàriament havia de ser en el lloc dels fets el dia D.
Però sabem que X era a la Patagònia el dia D, i no pot ser que fos a dos llocs tant distants
el mateix dia: contradicció!
Exemple: Demostrar (per contradicció) que per n ∈ QED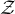 , si 3n + 2 és senar, llavors n és senar.
, si 3n + 2 és senar, llavors n és senar.
Demostració: Si contràriament fos 3n + 2 senar i n parell,
podriem escriure n = 2k per algún k ∈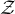 .
.
I tindriem 3n + 2 = 3(2k) + 2 = 6k + 2 = 2(3k + 1) amb la qual cosa 3n + 2 seria parell,
contradicció! Per tant no pot ser n parell, ha de ser n senar.
Observa que: Sovint una demostració per contradicció es pot reformular com una demostració per contraposició.__
∙ Demostrar que, Donats dos nombres naturals m,n, tots dos són senars si i només si el producte mn és senar.
Cal fer dues demostracions:
1.- m i n són senars ⇒ mn és senar. QED
Demostració: Demostració directa: Posem m = 2k1 + 1,n = 2k2 + 1.
Tindrem mn = (2k1 + 1)(2k2 + 1) = 4k1k2 + 2k1 + 2k2 + 1 = 2(2k1k2 + k1 + k2) + 1 que és
senar.
2.- m i n són senars ⇐ mn és senar. QED
Demostració: Demostració per contraposició: Si algún m o n no és senar, demostrarem que mn no és senar.
Posem que m és parell (si fos n qui és parell, els intrecanviem).
Llavors tenim m = 2k, i llavors mn = 2kn és parell. Per tant la contrapositiva és veritat.
∙ Demostrar que Donats dos nombres naturals m,n, si m + n és senar, llavors exactament un dels dos m o n és senar.
Tenim dues proposicions:
P : La suma m + n és senar.,
Q : Exactament un dels dos, m o n és senar,
i volem veure que P ⇒ Q.
És més senzill demostrar, per contraposició, que ¬Q ⇒ ¬P, és a dir que
¬Q : tots dos són senars o tots dos són parells,
¬P : la suma no és senar.
Demostració: Hi ha dos casos:
Cas 1.- Tots dos són senars: m = 2k1 + 1,n = 2k2 + 1,
Llavors m + n = 2(k1 + k2 + 1) és parell. QED.
Cas 2.- Tots dos són parells, m = 2k1,n = 2k2.
Llavors m + n = 2(k1 + k2) també és parell. QED
______
Per mostrar que una afirmació dels tipus “Tots els …compleixen …” és falsa, només cal trobar un cas que no ho compleix. Haurem provat que és veritable la contrària “Existeix un …que no compleix …”.
En diem un contraexemple.
Atenció: Un exemple no mostra que l’afirmació sigui veritable, un contraexemple sí mostra que és falsa!
Llegeix altre cop el capítol si no tens clar què vol dir la eficiència en termes Pareto.
Aquí ens interessa formalitzar els conceptes que apareixen. Posem que A1,A2 siguin dues assignacions factibles, és a dir que assignen a cada individu unes quantitats que no superen el disponible i denotem A1(i),A2(i) la utilitat que obté l’individu i segons les assignacions respectives.
Diem que A1 domina A2 si, per tots els individus, l’assignació segons A1 és més gran o igual que segons A2, és a dir que ∀i,A1(i) ≥ A2(i) . Escribim A1 ≽ A2 en aquest cas.
Llavors, si 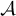 denota el conjunt d’assignacions factibles, diem que A⋆ és una assignació Pareto-eficient si
∀A ∈
denota el conjunt d’assignacions factibles, diem que A⋆ és una assignació Pareto-eficient si
∀A ∈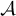 ,A⋆ ≽ A.
,A⋆ ≽ A.
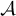 tal que A⋆ no domina A.
tal que A⋆ no domina A.
Els que el van conèixer el van estimar
Els que no el van estimar no el van conèixer.