Aquest és un document de treball INTERN, en fase de discussió i molt preliminar. No en feu difussió, sisplau.
(Enllaç al document principal)
(Enllaç a la versió pdf d’aquest document)
(Enllaç a la font LaTeX)
(Enllaç als fitxers de les figures)
El càlcul de derivades de funcions polinòmiques, potencials i racionals. Se’ls poden donar referències, exemples i eines (geogebra, WolframAlpha) per ajudar a repassar.
Per exemple, exercicis del IB-An&Appr 13-4:
amb les seves solucions
Cal posar l’èmfasi en els conceptes, la idea de mesurar el canvi, el creixement. Els exemples d’aplicació a l’economia i el cas de les epidèmies han de ser referents clau.
Donant per suposat que abans de la classe s’han mirat els materials proposats i han fet les activitats autònomes, es proposaran preguntes i clickers per provocar la reflexió i discussió en petits grups dels conceptes principals:
Si tenim y = f(x) i considerem l’interval [x1,x2], el quocient d’increments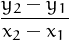 
= 
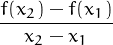es sol anomenar de
diferents maneres. Digues quines són correctes:
QUIZZ
= la variació de y entre x1 i x2
= la variació instantània de y en x = x1
== la variació mitjana de y entre x1 i x2.
== la ratio de canvi de y respecte x en l’interval [x1,x2]
== el quocient incremental de y respecte x en l’interval [x1,x2]
= la raó de canvis de y respecte x en el punt x1
== la raó de canvis de y respecte x en l’interval [x1,x2]
Discutim ara aquest exercici:
Solucions: 
Discutim quina és la resposta correcta i en cas d’incorrecta explica perquè i dona un exemple que ho mostri.
QUIZZ
Tenim y = f(x). Considerem l’interval [x1,x2] i el quocient d’increments Q =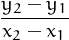 
= 
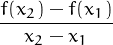== Si Q > 0, podem
assegurar que (f(x2) > f(x1)
= Si el quocient Q és negatiu, la funció és decreixent
= Si Q > 0, podem assegurar que el pendent de la gràfica en x = x1 és positiu.
== Si Q < 0 el segment que uneix els punts de la gràfica “fa baixada” = Si Q = 0, la gràfica és horitzontal.
QUIZZ
En el gràfic adjunt hi ha una funció i les seves dues primeres derivades, identifica-les.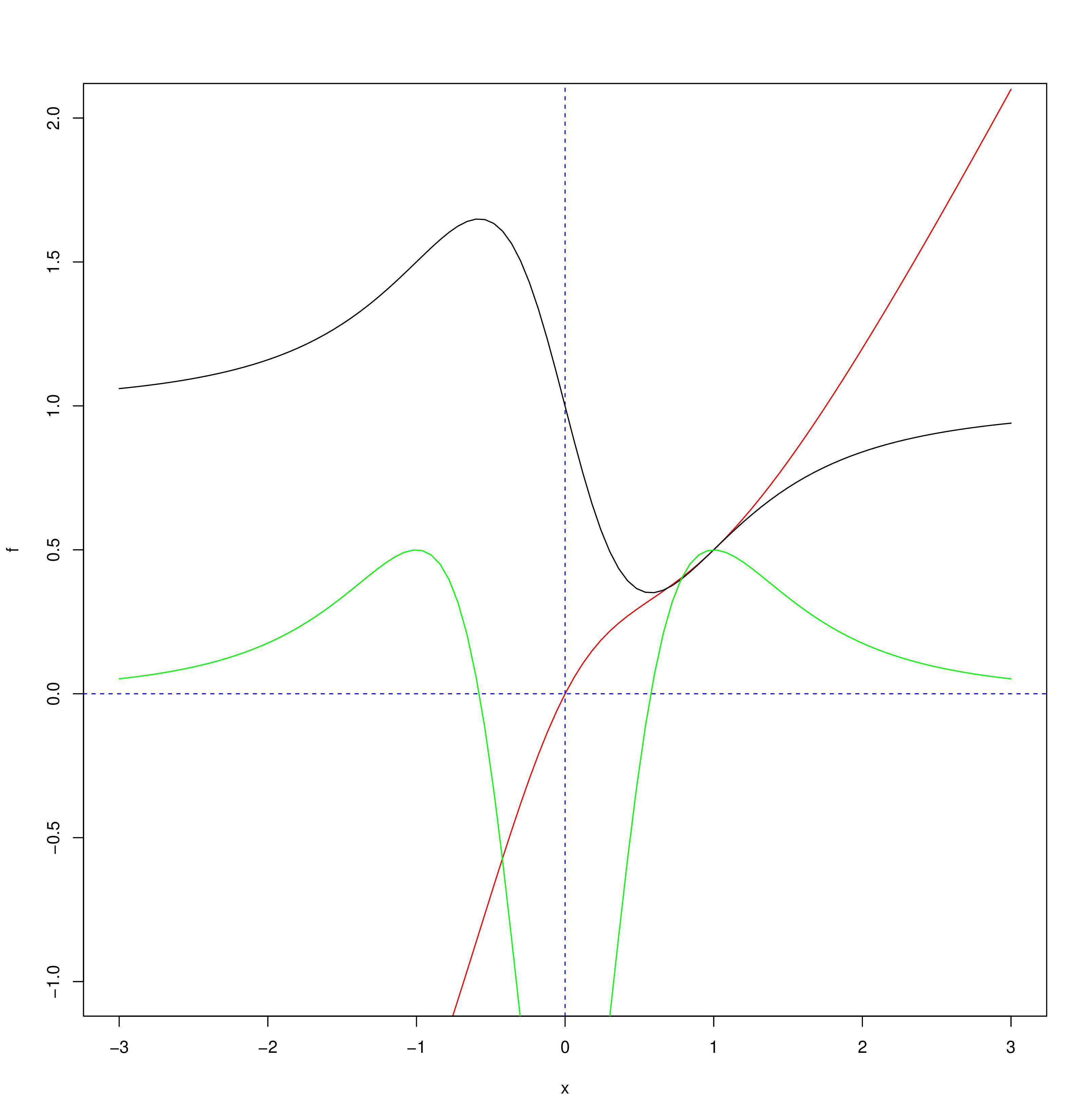 
A la col·lecció de preguntes de GoodQuestions Project de Cornell University, especialment a partir de la pàgina 15, hi ha moltes preguntes interessants per plantejar a classe per a la discusió.
Per exemple:
Answer: False. f′(0) equals the slope of the tangent at (0,0).
Answer: True. This gets students to think about tangent lines and derivatives. A vertical tangent line exists, although the derivative does not.
Answer: False. The limit limx→0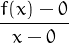
does not exist, because it equals -1 from the left, and 1 from the
right. Thus f′(0) does not exist.
Answer: True. Easy application of the limit definition of derivative. Students should note that close to 1, |x| = x. g′(1) = 2.
Capítols 6 i 10 del Pemberton&Rau.
Aquí recollim exemples de possibles activitats, per suposat que caldrà seleccionar-ne algunes i complementar-les amb d’altres ja disponibles.
Ja hem vist casos en què la variació d’una quantitat en funció d’una altra es pot descomposar a través de quantitats intermèdies. Per exemple, la variació del preu del petroli en dòlars segons el temps t en mesos pot ser Pd(t) = 20 + 0.4t durant un periode determinat. Però el valor de l’euro en funció del dòlar (que considerem constant en el temps) també és una funció que es pot expressar E(d) = 1.2d i per tant el preu del petroli en euros serà Pe(t) = E(Pd(t)). La variació del preu del petroli en euros serà
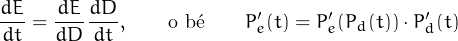
Això es pot explicar dient que si el preu en dòlars varia a raó de 0.4 dòlars/mes, i l’euro varia a raó de 1.2 euros/dòlar, la variació del petroli en euros serà de 0.4 × 1.2 euros per mes.
Com a regla general diem:
O bé: La derivada de la composta és
la derivada de la de fora (sense canviar la de dins)
multiplicada per
la derivada de la de dintre.
QUIZZ
El preu de la llimonada depén de la demanda P(D) però la demanda depén la temperatura D = D(T). Llavors, la variació del
preu en funció de la temperatura serà:
== P′(D) ⋅ D′(T)
= P′(D′(T))
= P′(D) + D′(T)
En el gràfic veiem el pes d’un bebè al llarg dels primers mesos de vida.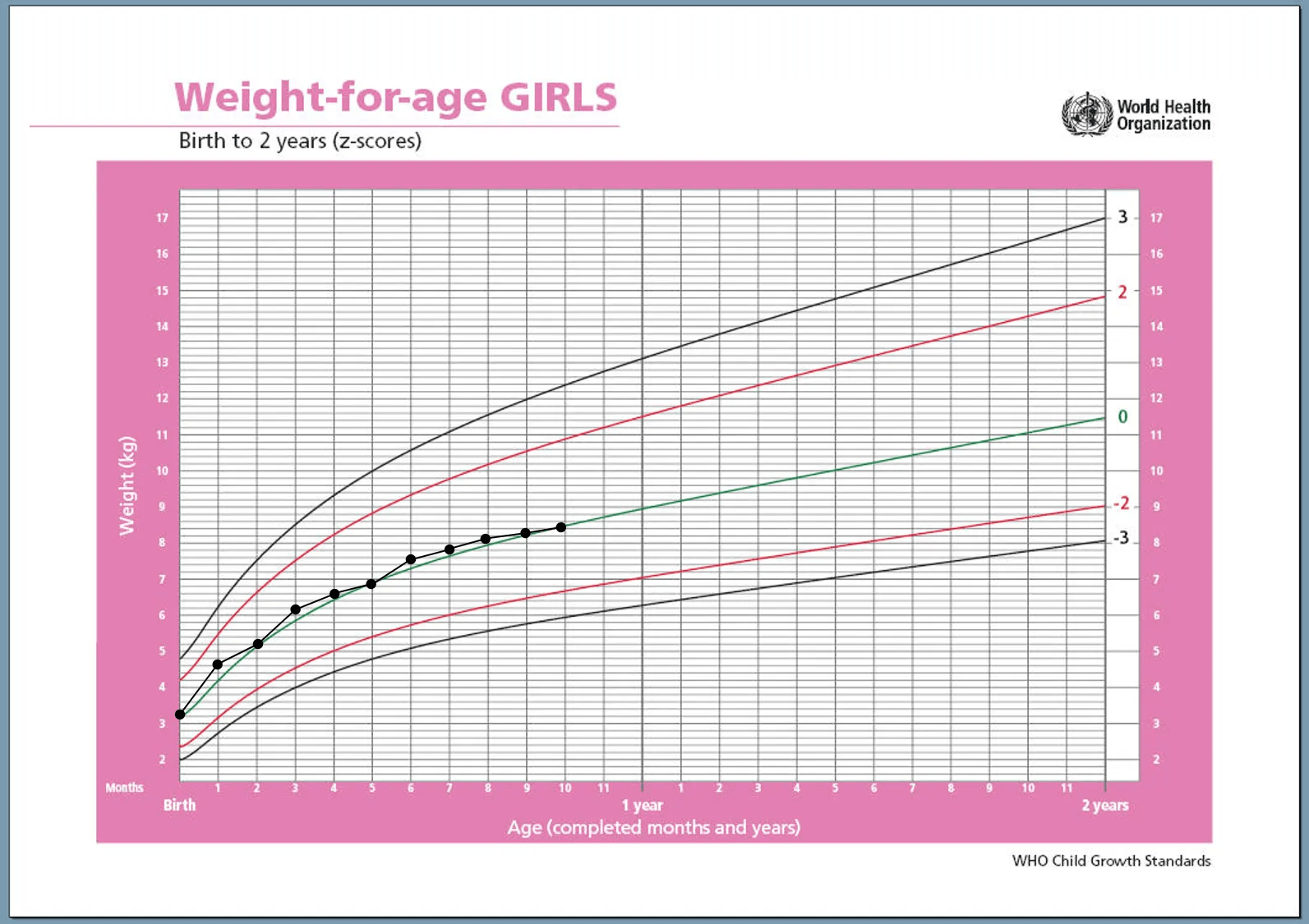 
En el mes 5 pesa 6.9 kg, i al mes 7 pesa 7,8 kg. En dos mesos ha augmentat 0,9 kg, el ritme de creixement en aquest periode és de 0,45 kg/mes. Per calcular-ho, dividim l’incement de pes (7,8-6,9=0,9) per l’increment del temps (7-5=2 mesos).
Aqui tenim també la gràfica de les alçades dels
bebès segons els mesos d’edad. De les diferents corbes
corresponents als diferent quantils (no entrem ara en aquest
tema) ens quedem amb la línia del mig, més gruixuda, que
correspon al bebè mitjà o promig.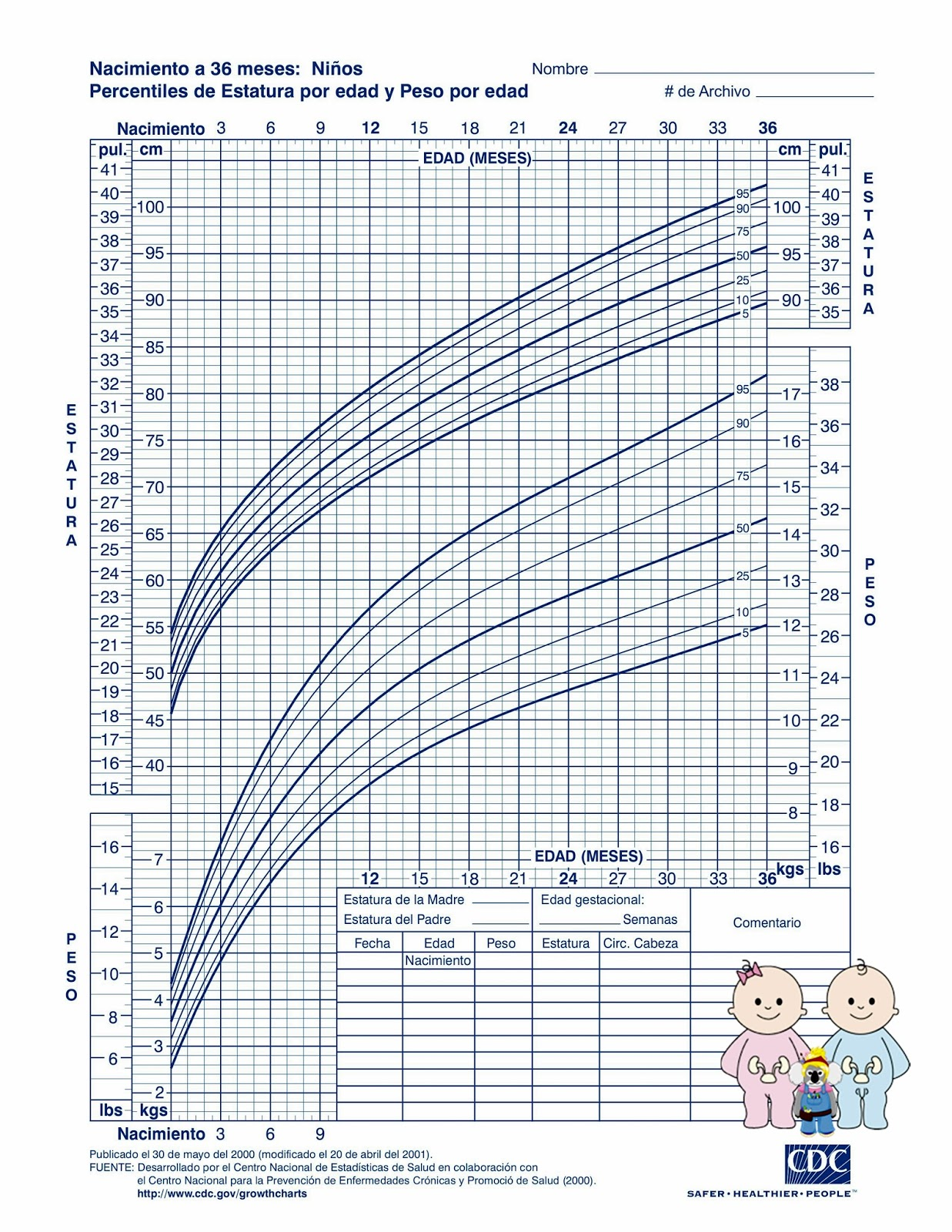 
Segons la taula, als 6 mesos el bebè tipus amida 67 cm, i als 9 mesos 74 cm. El seu creixement ha sigut de (74-67)/(9-6)=7/3, aproximadament 2,3 cm/mes. Altre cop calculem el quocient d’increments per calcular el ritme o raó decreixement.
Però el creixement no es produeix de cop, cada mes, sino que es produeix d’una manera continua. Això és el que reflecteix la corba suau que veiem a la figura anterior. Llavors, per amidar el ritme de creixement en un moment determinat, fem el quocient d’increments però el fem en interval de temps molt petits. Per exemple, si volem saber el ritme de creixement en el moment t = 5 mesos, prenem dos punts de la corba t = 5 i t = 5.1 i mirem com ha crescut el bebè en aquest curt periode, i calculem el quocient d’increments:
El ritme de creixment en t0 = 5 és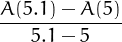 
El càlcul el podem veure més clar si prenem una funció senzilla A(t) = 55 + 4t0.2 i la grafiquem amb Geogebra. Podeu veure un exemple a https://www.geogebra.org/classic/q8wnqmbb:
etc...
En R podem fer
Mira’t aquests dos exemples de càlcul de la derivada utilitzant la definició:
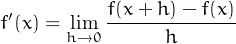
Ara repeteix el que has vist per demostrar que si f(x) = 2 -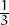 
x2, f′(x) = -
.
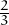O fes aquest 6.1.1. de PemRau: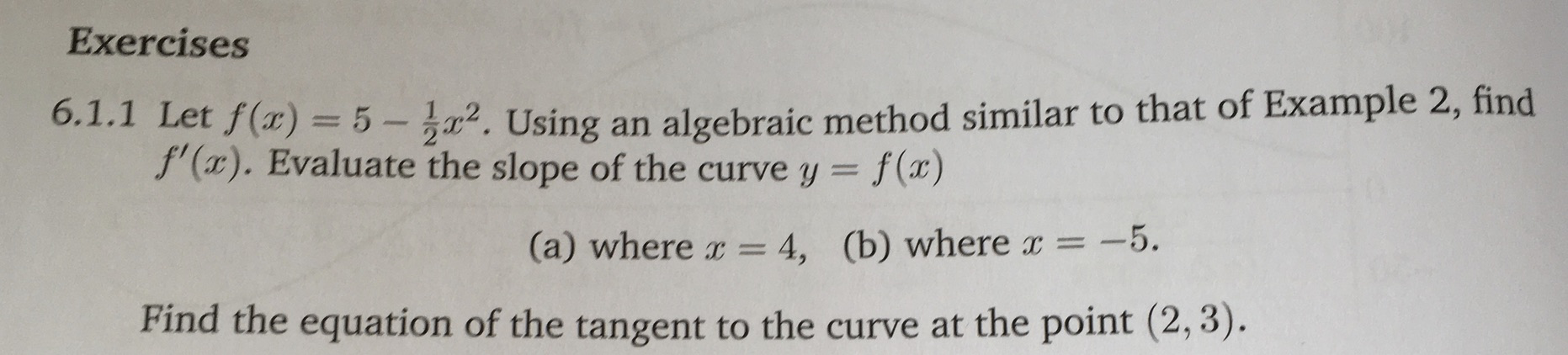 
Solució: 
Un exercici típic d’examen: Demostra fent servir la definició de la derivada com a límit del quocient d’increments, que per f(x) = a - bx2 on a i b són constants, es té f′(x) = -2b.
Com que f′(x0) ≈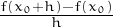
quan h és petit (en valor absolut), podem escriure f(x0 + h) - f(x0) ≈|h|f′(x0) quan |h| és
petit. Una altra manera d’escriure-ho: Si y = f(x), Δy = y′Δx.
(Repassa el capítol 6.2 de Pemb-Rau is no tens això gaire clar).
QUIZZ
Si el preu depén de la quantitat fabricada segons P = 2 + 5Q1∕3, calcula el preu marginal per Q = 3 i digues quan augmenta
el preu aproximadament si la quantitat passa de 3 a 3.01
== El preu augmentarà en 0.0080
= El preu augmentarà en 0.8012 [No, aixó és la derivada P′ per Q = 3]
Aquí pots veure com dibuixar la tangent a la gràfica d’una funció amb Geogebra.
Fes-ho tu ara per la funció f(x) =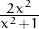 
i el punt a = 1.5. Porta el teu exemple al seminari.
Si fas una construcció com aquesta: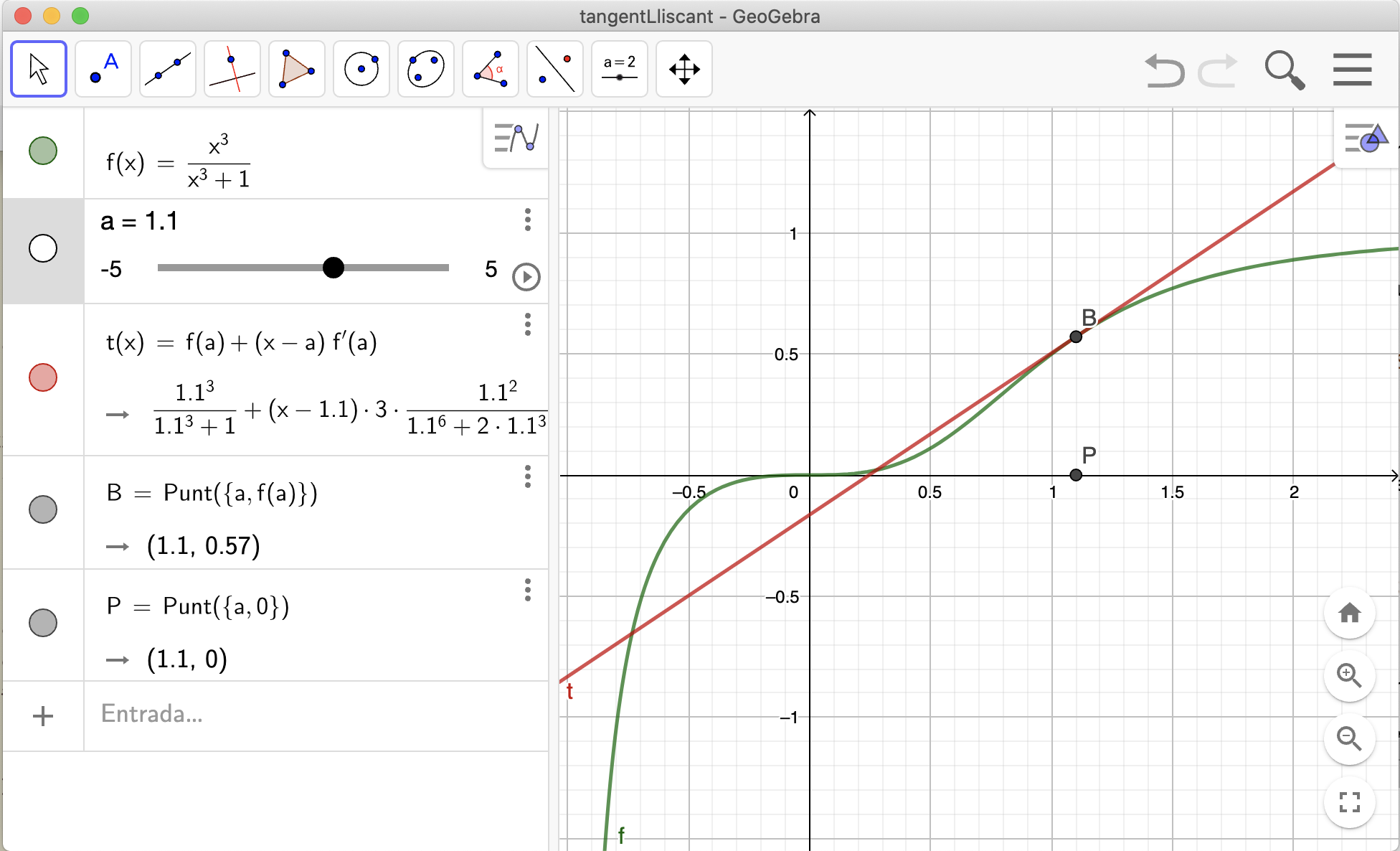 
podràs veure com canvia la tangent quan varia el punt x sobre el que es construeix la tangent.
Solució: https://www.geogebra.org/classic/sw8v57kc
R no sap fer derivades simbòlicament, però és molt potent numèricament. Podem demanar-li coses així:
auto
Cal fer això amb precaució: enlloc de la derivada estem calculant el quocient incremental per un increment petit, però “petit” no és una especifiació sempre vàlida, segons quina sigui la funció i el punt on es calcula pot haver-hi errors no menyspreables.
En el tema 6. Teoremes de Bolzano, valors extrems vem veure com obtenir solucions a equacions amb el mètode de bisecció. Un mètode molt més eficient es pot trobar si enlloc de passar cada vegada d’un interval a la meitat s’aprofita el fet que la derivda ens dona una bona aproximació de la funció.
Llegeix aquestes pàgines del llibre de text: Pem-Rau.
…
QUIZZ
El mètode de Newton...
Amb Geogebra podem veure fàcilment com treballa el mètode de Newton:
Un exercici típic d’examen: Demostra fent servir la definició de la derivada com a límit del quocient d’increments, que per f(x) = a + bx2 on a i b són constants, es té f′(x) = 2b.
