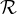n, però aquí es vol introduir la
visió abstracta de l’estructura d’espai vectorial. Naturalment, només una pinzellada per obrir gana als estudiants que puguin
copsar-la.
Aquest és un document de treball INTERN, en fase de discussió i molt preliminar. No en feu difussió, sisplau.
(Enllaç al document principal)
(Enllaç a la versió pdf d’aquest document)
(Enllaç a la font LaTeX)
(Enllaç als fitxers de les figures)
A temes anteriors s’han vist ja els vectors del pla i de l’espai, aquí seguiran servint com a exemples bàsics sobre els que fonamentar la intuïció.
En temes anteriors s’han vist els vectors del pla i de l’espai, potser en algun cas vectors de 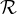n, però aquí es vol introduir la
visió abstracta de l’estructura d’espai vectorial. Naturalment, només una pinzellada per obrir gana als estudiants que puguin
copsar-la.
En aquest i el següent tema es pretén introduir (o reforçar) la capacitat d’abstracció matemàtica amb els conceptes d’espai vectorial general i la manipulació algèbrica de símbols que representen vectors o matrius.
És molt probable que a alguns estudiants aixó els costi molt d’assolir, se’ls requerirà com a mínim que aprenguin les definicions i propietats bàsiques, però l’objectiu del plantejament ha de ser que alguns estudiants vegin com el procés de definició-propietats-teoremes permet construir un entramat de conceptes aplicables a diferents contextos sòlidament.
El fet que dues bases tenen el mateix nombre d’elements s’acceptarà sense demostració. A partit d’aquí sí que es poden demanar petites demostracions de molts fets interessants.
Cal insistir en les demostracions, senzilles per suposat, però importants per mostrar la solidesa formal.
El tema es plantejarà a partir de la definició d’EV, mostrar-ne exemples: 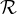n, Polinomis de grau fins a n, funcions derivables,
matrius m × n etc.
Pensant en els videos que els recomanem, s’aclarirà que cal diferenciar els vecors dels escalars per la notació que s’hi empri,
sigui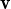 
, , v o la que sigui.
A partir dels axiomes, es deduiran propietats simples com ara 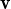0 ⋅
= 0
Definició de subespai, de CL en general, d’espai generat per un conjunt de vectors.
Definició d’IL. Crec que ens parem aquí. En els temes d’àlgebra matricial i de diagonalització es podrà aplicar i ampliar una mica.
El tema plantejat en abstracte no apareix en els llibres de text que utilitzem normalment. Caldrà escriure un breu resum de les definicions i propietats que volem que adquireixin, que no són moltes.
Pot servir de referència (avançada) ÀLGEBRA LINEAL, ApuntsFMEBarcelona, Gener 2019, de Andreu Boix, Paolo Lammens, FME-UPC. https://apuntsfme.gitlab.io/pdfs/primer/algebra_lineal.pdf
VECTOR SPACES - LINEAR ALGEBRA https://www.youtube.com/watch?v=XDvSsDsLVLs 13min TheTrevTutor
Abstract vector spaces — Essence of linear algebra, chapter 15 https://www.youtube.com/watch?v=TgKwz5Ikpc8 16min 3Blue1Brown. Esmenta alguns conceptes que no hem vist encara, però l’enfocament és interessant.
The tools of linear algebra are extremely general, applying not just to the familiar vectors that we picture as arrows in space, but to all sorts of mathematical objects, like functions. This generality is captured with the notion of an abstract vector space.
Visualització en geogebra. https://youtu.be/uiz5_nKO0-E
Podem aprofitar exercicis de http://www.xtec.cat/~dcastell/webatxillerat/ev/evexeresolts.htm.
A la pàgina 12 dels apunts de la U. d’Alacant (més avall) també hi ha una colecció d’exercicis aprofitables.
Cal pensar exercicis del tipus:
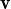1,
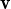2,…,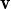
n d’un espai vectorial que són linealment independents, demostrar que si subtituïm
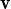1 per 
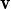1 +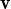 
2 el conjunt de vectors resultant segueix essent linealment independent.
,
,
,
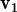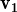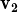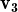} és LD.
,
,
+ 
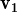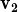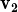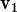} és LD.
Pot servir de referència (avançada) ÀLGEBRA LINEAL, ApuntsFMEBarcelona, Gener 2019, de Andreu Boix, Paolo Lammens, FME-UPC. https://apuntsfme.gitlab.io/pdfs/primer/algebra_lineal.pdf
El text ELEMENTS D’ÀLGEBRA LINEAL de Xaro Soler Escrivà, Universitat d’Alacant, és més senzill, té molts exemples i exercicis però se salta moltes demostracions.