Diagonalitzaci, aplicacions

Diagonalització, aplicacions

Projecte Math21, Departament Economia i Empresa, UPF

25 de març de 2021

Índex

1 Objectius d’aprenentatge
2 Prerequisits
3 Guia pel professor
3.1 Presentació del tema
3.2 Materials bàsics
4 Activitats autònomes
4.1 Clickers
  4.1.1 act1
  4.1.2 Càlcul de auto-vv amb Geogebra, R
5 Llista d’exercicis
  5.0.1 Exercici, per exemple,
6 Suplements avançats
7 Exercicis per exàmens

Aquest és un document de treball INTERN, en fase de discussió i molt preliminar. No en feu difussió, sisplau.

(Enllaç al document principal)
(Enllaç a la versió pdf d’aquest document)
(Enllaç a la font LaTeX)
(Enllaç als fitxers de les figures)

1 Objectius d’aprenentatge

Auto vectors/valors, propietats
Teorema espectral
Classificació de FQ segons valors propis, regla de Descartes
Concavitat/convexitat de formes quadràtiques

2 Prerequisits

3 Guia pel professor

Es donarà molta més importància a les petites demostracions de les propietats dels auto-valors/vectors que no pas al seu càlcul.

El càlcul es mostrarà en alguns casos senzills i es deixarà per Geogebra, R o wolframAlpha.

3.1 Presentació del tema

3.2 Materials bàsics

4 Activitats autònomes

4.1 Clickers

Se’n poden trobar a https://pi.math.cornell.edu/~maria/gq/str.pdf a partir de la pàgina 28.

Aquí recollim exemples de possibles activitats, per suposat que caldrà seleccionar-ne algunes i complementar-les amb d’altres ja disponibles.

4.1.1 act1

4.1.2 Càlcul de auto-vv amb Geogebra, R

Amb geogebra, les matrius s’entren en la forma {{2,1,2},{1,1,-1},{2,-1,0}}. Aquí fem servir la finestra CAS de Geogebra, recorda que per donar nom a un matriu hem d’escriure A := ….

Amb R, (cal adaptar això)

##########################
## valors i vectors propis
##########################
> A = matrix(c(2,1,2,1,1,-1,2,-1,0), nrow = 3)
> A
     [,1] [,2] [,3]
[1,]    2    1    2
[2,]    1    1   -1
[3,]    2   -1    0
> eigs = eigen(A)  # o qualsevol nom que ens agradi
> names(eigs)  # eigs te ara dos components:
[1] "values"  "vectors"
> eigs$values
[1]  3.292402  1.602705 -1.895107
> eigs$vectors
          [,1]        [,2]       [,3]
[1,] 0.8642795 -0.07589338  0.4972536
[2,] 0.1705987 -0.88573564 -0.4317041
[3,] 0.4731987  0.45794385 -0.7525758
## els vectors van en columnes
## comprovem que la columna 1 i la columna 2 son ortogonals:
> sum(eigs$vectors[,1]*eigs$vectors[,2])
[1] 9.714451e-17
> eigs$vectors %*% t(eigs$vectors)
             [,1]          [,2]          [,3]
[1,] 1.000000e+00  1.110223e-16  1.110223e-16
[2,] 1.110223e-16  1.000000e+00 -3.330669e-16
[3,] 1.110223e-16 -3.330669e-16  1.000000e+00

QUIZZ
Explica el que hem fet a la darrera instrucció del llistat anterior i el resultat que hem obtingut.

A WolframAlpha, només cal entrar la matriu, també en la forma {{2,1,2},{1,1,-1},{2,-1,0}} i ens dona molta informació, determinant, inversa, eigenvalues (valors propis), eigenvectors (vectors propis), etc.

Les capacitats simbòliques de WolframAlpha ens permeten treballar amb matrius que depenen d’algun paràmetre, per exemple,

5 Llista d’exercicis

5.0.1 Exercici, per exemple,

Utilitzant WolframAlpha o similar, digues per a quins valors de a la matriu

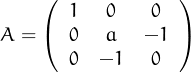
( ) ( 1 0 0 ) A = 0 a -1 0 -1 0

té un valor propi doble.

Solució: Per a = ±2

6 Suplements avançats

Es podria plantejar la SVD?

7 Exercicis per exàmens

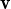Demostra que si λ, és un eigen parell, k 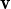és vector propi amb el mateix valor propi.
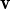És cert que si λ, és un eigen parell, llavors kλ també és valor propi amb vector propi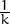 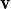. Si és cert, demostra-ho, si no, dona un contraexemple amb una matriu de 2 × 2.