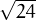Índex

1 Objectius d’aprenentatge

• Concepte de funció, domini, recorregut, gràfica
• Funcions lineals, equació de la recta, intersecció de rectes, equacions i inequacions lineals
• Elements de programació lineal
• La funció valor absolut, la funció f(x) = |x|∕x
• Funcions quadràtiques, paràboles, completar el quadrat, desplaçament de y = x².
• Transformacions de gràfiques: reflexions en els eixos, translacions, canvis d’escala en els eixos
• Ús de geogebra o eines equivalents en aquests items

2 Prerequisits

• Arrel quadrada, regles de potenciació
• L’àlgebra elemental de resolució d’equacions lineals o de segon ordre
• Les beceroles de geogebra

3 Guia pel professor

3.1 Presentació del tema

3.2 Materials bàsics

Les transparències d’Àngel Gil Guia 1. Introducció. Funcions

Pels Elements de programació lineal, la secció 2.3 del PermRau.

Capítol 2 Functions de IB-HL-MAth-An&Appr. També Capítol 2 Functions de IB-HL-MAth-Appl&Interp.

4 Activitats autònomes

4.0.1 Fer gràfiques amb l’ordinador

Amb Geogebra és fàcil, només escriure la definició, per exemple f(x)=abs(x) o bé directament f(x)=|x|, ja apareix el seu gràfic a la finestra gràfica. Després podem decidir si volem veure’l o no amb el botnoet de color de l’esquerra, i podem canviar-ne alguns comportament amb la opció Configurar del menú de la seva dreta.

Amb WolframAlpha, també és fàcil: escrivim plot abs(x), {x,-1,1} i si no volem dir els límits de l’eix x podem ometre la segona part.

Amb R cal que la funció tingui un nom, i la variable independent no la donem. Si cal, haurem primer de definir la funció i donar-li un nom. Prova aquestes comandes:

Practica una mica, hauries de ser capaç de reproduir aquests gràfics amb qualsevol dels paquets de software comentats.

QUIZZ
Fes correspondre a cada gràfica una de les definicions de sota i digues quines són les gràfiques que no poden correspondre a una funció. De fet, hi ha dues d’aquestes gràfiques que no poden ser la gràfica d’una funció, quines són?

Solució: B: x = -3, K: x² + y² = 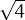no són funcions y = f(x)

Solució:

4.0.2 Completar el quadrat amb Geogebra

Aquest és un cas clar de tema que no es toca a classe, ni potser al seminari, se’ls fa treballar autònomament, se’ls pot preguntar als seminari si ho han fet, i pot sortir a un examen tipus pregunta curta..

Per interpretar correctament un polinomi quadràtic com ara p(x) = x² + 3x - 1 és molt còmode competar el quadrat, és a dir escriure’l en la forma p(x) = (x - a)² + b. Aixó ho podem fer pas per pas així:

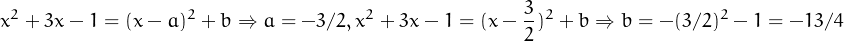
Podem entrar en Geogebra directament  p(x)=A (x-a)^2 + b i se’ns creen variables A,a,b de manera que després podem veure l’efecte de fer variar els seus valors. També podem posar p0(x)=x^2 per tenir la referència de la paràbola estàndard. Fixa’t que per Geogebra A i a són variables diferents.

Fes-ho i contesta:

QUIZZ
Quan fem variar a la paràbola p(x) es desplaça verticalment SI/NO
Quan fem variar b, la paràbola p(x) es desplaça verticalment SI/NO
Si a > 0 la paràbola p(x) s’ha desplaçat a la dreta respecte la p₀ SI/NO
Si A < 0 la paràbola té les banyes cap avall SI/NO
Si A = 0 la paràbola sempre està a la part positiva de l’eix vertical SI/NO
Mantenim A = 1 i fem variar b. Llavors, la paràbola p(x) té dos zeros si i només si b < 0 SI/NO

QUIZZ
Observant que p(x) = x² + 3x - 1 = (x - 3∕2)² - 13∕4, es pot deduir que
== p(x) = 0 ⇔ x = ±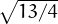 + 3
= p(x) = 0 ⇔ x = ±(13∕4)² + 3
= p(x) = 0 ⇔ x = ±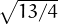 - 3
= cap de les anteriors

De fet, Geogebra ens pot fer la compleció del quadrat automàticament. Asseguraeu-vos que esteu en la finestra CAS de Geogebra (CAS vol dir Computer Algebra System, Sistema de computació algèbrica, algunes versions de Geogebra en diuen directament la Finestra Algebraica). A la finestra CAS les lletres es tracten com a símbols que poden representar nombres però que no tenen un valor fix, tal com ho fem en l’àlgebra habitual.

Llavors podreu provar coses com això

4.0.3 Desigualtats lineals

4.0.4 Programació lineal: enfocament gràfic

Es pot repassar el que saben de representació gràfica de rectes i de desigualtats lineals per introduir les idees bàsiques de la programació lineal. Es pot seguir la línia de PembRau, cap. 2.2 i 2.3, pàgines 26-35.

5 Llista d’exercicis

5.0.1 Exerc-complQuad

En el cas que tinguem p(x) = Ax² + Bx + C, amb A≠1 per completar el quadrat com hem fet a 4.0.2 caldrà primer treure la A com a factor comú: p(x) = A(x² + 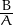x + 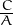), i després ja podem procedir com abans.

• Aplica-ho per completar el quadrat de p(x) = 2x² + 3x - 4
• Aplica-ho en general per p(x) = Ax² + Bx + C
• Dedueix del que has fet a (b) la manera de trobar els zeros de p(x).

5.0.2 Exerc-complQuad

Hem vist a 4.0.2 que en completar el quadrat de Ax² + Bx + C = 0 obtenim

6 Suplements avançats

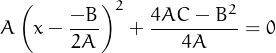
No crec que hi hagi temps de veure gaire cosa de polinomis generals (d’orde més gran de 2). Es pot referir els estudiants avançats a:

1. S&H-MAE: XXX
2. IB-An$Appr

7 Exercicis per exàmens

7.0.1 Troba la transformació

En el capítol 3.5 Toma de decisiones y escasez del llibre de text de Introducció a la Microeconomia apareix aquesta figura on es veu la frontera factible del problema de decissió que s’hi planteja.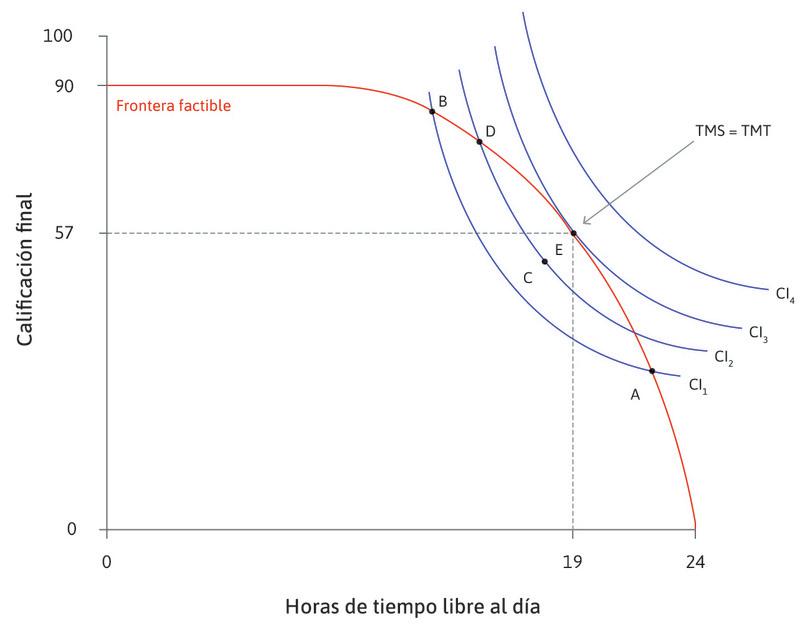

Utilitzant una funció del tipus y = f(t) = A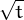, quina transformació hi podries aplicar per obtenir la frontera factible de la imatge?

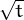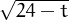Solució: Podem partir de y = A, canviem el signe a la variable independent per fer una reflexió respecte l’eix vertical i li sumem 24 per desplaçar-la cap a la dreta i fer que el tall amb l’eix horitzontal sigui a x = 24. Tenim ara y = A, per tal que y(0) = 90 caldrà prendre A = 90∕