Índex

1 Objectius d’aprenentatge

• Composició de funcions, funció inversa
• Funcions potencials, y = ax^b comportament segons els valors de a,b
• Corbes d’isonivell
• Desigualtats, inequacions
• Encara transformacions de gràfiques

2 Prerequisits

3 Guia pel professor

Es tracta d’ampliar el que s’ha vist al tema I-2 afegint conceptes importants com la composició, la inversa.

Les funcions potencials apareixen constantment en el model econòmics que estan estudiant en paralel a IntroMicro. En particular, les corbes de isobenefici i similars. Per això convé introduir ja la idea de corba de nivell sense entrar gaire en les funcions de dues variables.

3.1 Presentació del tema

3.2 Materials bàsics

4 Activitats autònomes

4.0.1 Videos sobre composició de funcions

De la Kahn Academy:

Introduction to function composition — Functions and their graphs — Algebra II — Khan Academy (6min)

Evaluating composite functions example — Functions and their graphs — Algebra II — Khan Academy (4min)

Creating new function from composition — Functions and their graphs — Algebra II — Khan Academy (3 min)

Sobre funció inversa: Introduction to function inverses — Functions and their graphs — Algebra II — Khan Academy (9 min)

Després de veure aquests videos, respón aquestes qüestions:

QUIZZ
Si f(x) = |x| i g(x) = x - 2 i posem h = f ∘ g (ho llegim f després de g) aleshores
==h(x) = |x - 2|
= h(x) = |x| - 2
= qualsevulla de les dues pot ser veritat.

4.0.2 Funcions compostes

Llegeix i practica les pàgines 24-28 del llibre IB-HL-AnAppr:

Les solucions:

4.0.3 Funcions potencials

Fes correspondre cada gràfica a cadascuna de les funcions potencials que es llisten:

Solució:

4.0.4 Desigualtats amb potencials

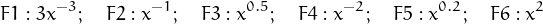
Prenem aquests fet sense demostració:

• Si x < y i a > 0 aleshores ax < ay.
• Si x < y i a < 0 aleshores ax > ay.
• Si x < y, aleshores x^-1 > y^-1

A partir d’això, podem per exemple, demostrar que
Fet 4: Si 0 < x < y i 0 < a < b aleshores ax < by.
Demostració
Multiplicant 0 < x < y per a i 0 < a < b per y, obtenim ax < ay i ay < by del que es desprén que ax < by. □

Ara podem fer servir el Fet 4 per demostrar que
Fet 5: Si 0 < x < y aleshores x² < y² i també xⁿ < yⁿ per qualsevol nombre natural n > 0. La demostració és immediata, només cal multiplicar la primera desigualtat del Fet 4 per ella mateixa, i per demostrar la segona part caldrà multiplicar-la per ella mateixa n vegades. □

El Fet 3 es pot veure clar gràficament: la gràfica de la funció y = 1∕x és sempre decreixent, és a dir, si ens desplacem d’esquerra a dreta , els valors de y creixents, la gràfica “fa sempre baixada”. Comprova-ho ara fent la gràfica amb Geogebra o similar.

Aquest Fet 3 es pot demostrar per contradicció: si fos cert que x < y i que x^-1 < y^-1, multiplicant les dues expressions i segons el Fet 4, tindriem 1 < 1 que és ben fals!

Wolfram Alpha resol les inequacions, tot i que de vegades el resultat que dona pot ser difícil d’interpretar. Com interpretes aquest resultat? Intenta resoldre tu la ineqüació

i comprova-ho.

4.0.5 Una funció de producció potencial

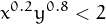
De fet aquí R és una micaprematur, si estem a la setmana 3 del curs potser encara no l’han vist gaire.

En el tema 3.1 Trabajo y producción del llibre de text de Introducció a la macroeconomia heu vist un exemple de funció de producció del tipus y = f(h) = Ah^α amb A > 0 i 0 < α < 1.

Dibuixa amb Geogebra o amb R el gràfic d’aquesta funció per diferents valors de A i de α.

Amb R pots fer servir aquest codi (copia’l a la finestra del R Script per poder modificar-lo)

En Geogebra, hauries de ser capaç de reproduir això:

(solució: vegeu https://www.geogebra.org/calculator/z5gbxwvt)

QUIZZ
En R, fem servir la ordre abline(a, b)
= per dibuixar la recta que passa per a i per b
= per dibuixar la recta de pendent b i que talla l’eix horitzontal per x = a
== per dibuixar la recta de pendent b i que talla l’eix vertical per y = a
= cap de les altres

QUIZZ
Per dibuixar el producte mitjà del treball fem servir la ordre Derivada
= tant en R com en Geogebra
== en Geogrbra, però no en R
=en R però no en Geogebra
= en cap dels dos.

QUIZZ
La funció de producció que planteja el Leibniz que has llegit és tal que si Alexei dedica moltíssimes hores de treball, mai aconseguirà superar la qualificació de 9. La funció que fa servir després en l’exemple
= s’assembla a la desitjada però permetria que Alexei obtingués més de 20 si hi dediqués unes 300 hores
== per obtenir un 10 hauria de dedicar-hi unes 214 hores
= per resoldre l’equació f(h) = 10 cal fer servir logaritmes.

4.0.6 Corbes de isonivell

Sovint tenim dues quantitats x,y lligades per una funció y = f(x) però que també ens donen una tercera quantitat z = f(x,y), és a dir, que donats valors de x,y podem calular el valor z associat. Això ho esteu trobant en exemples aplicats a la microeconomia.

Per exemple, refresca el capítol 3.2 Preferencias i en concret el Leibniz sobre les corbes d’indiferencia on es considera la funció d’utilitat U(t,y) on t són les hores de temps lliure d’Alexei, i y és la nota de l’examen que obté i que depèn de les hores que no dediqui a temps lliure: y = y(t).

La formulació matemàtica que proposen: U(t,y) = t^αy^β (és una funció tipus Cobb-Douglas).

Les corbes d’indiferència U(t,y) = c són els punts on la utilitat és la mateixa, c, en diem també corbes de nivell o corbes de isonivell. En la figura pots veure com visualitzar les corbes d’isonivell en Geogebra.

Si tenim U(t,y) = c, com que U(t,y) = t^αy^β, podem expressar y en funció de t. Per aïllar la y en t^αy^β = c dividim a le dues bandes per t^α i tenim y^β = ct^-α i si ara elevem els dos termes de la igualtat a 1∕β, tenim

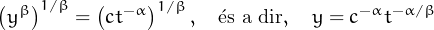
QUIZZ
Aplica això al cas U(t,y) = .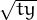
Obtindrem:
== y = c²t^-1
= y = ct^-1
= y = ct^-2
= cap de les anteriors

Tornarem a aquest exemple més endavant per discutir aspectes associats amb les derivades.

5 Llista d’exercicis

1. Si f(x) = ax + b i g(x) = cx + d i es compleix f ∘ g = g ∘ f, demostra que (a - 1)d = (c - 1)b.
2. Si f(x) = x^a, calcula i simplifica f(f(x)).
3. Si f(x) = x^a, calcula i simplifica f^-1(x).
4. Si f(x) = x^a i g(x) = x^b demostra que es compleix f ∘ g = g ∘ f.

5.0.1 Desigualtats amb potencials

1. Fent servir els fets expressats a 4.0.4, demostra que:
   Si 0 < x < y, per tota n > 1, x^-n > y^-n
2. Explica, a partir de la seva gràfica, si la funció y = x^a per x > 0 i amb a > 0 és creixent o decreixent segons siguin els valors de a.
3. En el context i notacions de 4.0.6 i suposant t,y > 0 com és habitual en Micoreconomia, aïlla la t de la inequació U(t,y) < c. Tingues bé en compte els fets sobre desigualtats i potències que hem vist abans (4.0.4)

5.0.2 Exercici

6 Suplements avançats

7 Exercicis per exàmens