Teoremes de Bolzano, valors extrems

Projecte Math21, Departament Economia i Empresa, UPF

25 de març de 2021

Índex

1 Objectius d’aprenentatge
2 Prerequisits
3 Guia pel professor
3.1 Presentació del tema
3.2 Materials bàsics
  3.2.1 Good Questions
4 Activitats autònomes
  4.0.1 Teorema de Bolzano
  4.0.2 act1
5 Llista d’exercicis
  5.0.1 Exercici
6 Suplements avançats
7 Exercicis per exàmens

Aquest és un document de treball INTERN, en fase de discussió i molt preliminar. No en feu difussió, sisplau.

(Enllaç al document principal)
(Enllaç a la versió pdf d’aquest document)
(Enllaç a la font LaTeX)
(Enllaç als fitxers de les figures)

1 Objectius d’aprenentatge

Teorema de Bolzano
Solució numèrica d’equacions: l’algoritme de bisecció
Algoritme de la falsa posició
Conjunts tancats, oberts
Conjunts convexos, compactes

2 Prerequisits

3 Guia pel professor

3.1 Presentació del tema

3.2 Materials bàsics

3.2.1 Good Questions

Del projecte del Dept of Mathematics de la Cornell U.

4 Activitats autònomes

4.0.1 Teorema de Bolzano

Video que explica de manera senzilla el Teorema de Bolzano Bolzano’s theorem /explanation and examples by Philip Gorick.

Un video que explica i demostra formalment el Teorem de Bolzano: Bolzano’s theorem, Proof and Applications by discovermaths.

Un altre que parla del teorema del valor intermedi, una versió lleugerament diferent però equivalent del teorema Intermediate value theorem to prove a root in an interval (KristaKingMath) (5min)

QUIZZ
El teorema de Bolzano, per una funció definida en un interval tancat [a,b], amb f(a) ⋅ f(b) < 0
= diu que si existeix algun punt c ∈[a,b] amb f(c) = 0 llavors f és continua
= diu que no pot existir un punt c ∈[a,b] amb f(c) = 0 si f no és continua
= diu que existeix un únic punt c ∈[a,b] amb f(c) = 0 si f és continua
== cap de les anteriors

QUIZZ
Si considerem la funció y = f(x) = 1∕x en l’interval [-1,1]
== No es pot aplicar el T. de Bolzano perquè la funció no és continua en l’interval
= No es pot aplicar el T. de Bolzano perquè l’interval no és tancat
= No es pot aplicar el T. de Bolzabo perquè la funció no canvia de signe en l’interval
= El t. de Bolzano ens assegura que hi ha algún c ∈[-1,] tal que f(c) = 0.

El t. de Bolzano ens assegura l’existència d’una arrel de la funció, però, com la hem de calcular?

El mètode de bisecció és molt util, i molt eficient, per trobar solucions numèriques a equacions, especialment en casos en què la solució numèrica pot ser molt complicada. Per exemple, no sabem resoldre equacions com ara x² + √--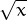
x = 1, i segurament no existeix cap mètode per resoldre-les de manera exacta algèbricament, però podem començar dibuixant-ne el gràfic i després resoldre-les numèricament, és a dir, buscant un valor aproximat, tant aproximat com ens interessi.

Mira’t aquest video sobre el mètode de bisecció How to locate a root — Bisection Method — ExamSolutions, by ExamSolutions (12 min)

Ara fes-ho amb R, fent servir aquest codi o similar:

f= function(x) x^2+sqrt(x)-1
f(0:10)
plot.function(f,0,1)

a= 0
b=1

print("a, (a+b)/2, b")
print(c(a,(a+b)/2, b))
print(c(f(a), f((a+b)/2), f(b)))

# i segons on veiem el canvi de signe, canviem a o b
a = (a+b)/2
# o be
b=(a+b)/2

auto

> a <- 0
> b <- 1
> print("a, (a+b)/2, b")
[1] "a, (a+b)/2, b"
> print(c(a,(a+b)/2, b))
[1] 0.0 0.5 1.0
> print(c(f(a), f((a+b)/2), f(b)))
[1] -1.00000000 -0.04289322  1.00000000
> a=(a+b)/2
> print("a, (a+b)/2, b")
[1] "a, (a+b)/2, b"
> print(c(a,(a+b)/2, b))
[1] 0.50 0.75 1.00
> print(c(f(a), f((a+b)/2), f(b)))
[1] -0.04289322  0.42852540  1.00000000
> b=(a+b)/2
> print("a, (a+b)/2, b")
[1] "a, (a+b)/2, b"
> print(c(a,(a+b)/2, b))
[1] 0.500 0.625 0.750
> print(c(f(a), f((a+b)/2), f(b)))
[1] -0.04289322  0.18119442  0.42852540

Segueix repetint el procés i aruat’t quan estiguis segur de quina és la primera xifra decimal de l’arrel que estem buscant.

QUIZZ
Digues entre quins límits està l’arrel quan t’has aturat:
== Entre 0.50000 0.53125
= Entre 0.515625 0.531250
=Entre 0.500000 0.515625

De fet, tant R com Geogebra tenen implementat aquest mètode (o d’altres una mica més sofisticats que no veurem. Així, per trobar l’arrel de la funció f(x) = e^-x - x, és a dir, per resoldre l’eqüació e^-x = x, en R pots teclejar uniroot(function(x)exp(-x)-x, c(0,5)) on li hem dit que la busqui entre 0 i 5. El resultat ´s molt informatiu, però de moment ens quedem amb l’arrel (root en anglès) que és 0.5671674.

En Geogebra, podem teclejar simplement Arrel(exp(-x)-x) i si estem en mode aproximat obtindrem 0.57

QUIZZ
Fent servir aquestes ordres, en R o en Geogebra, digues el valor de x que satsifà l’eqüació x^0.8 - x^0.2 - 1 = 0.