Aquest és un document de treball INTERN, en fase de discussió i molt preliminar. No en feu difussió, sisplau.
(Enllaç al document principal)
(Enllaç a la versió pdf d’aquest document)
(Enllaç a la font LaTeX)
(Enllaç als fitxers de les figures)
Aquí recollim exemples de possibles activitats, per suposat que caldrà seleccionar-ne algunes i complementar-les amb d’altres ja disponibles.
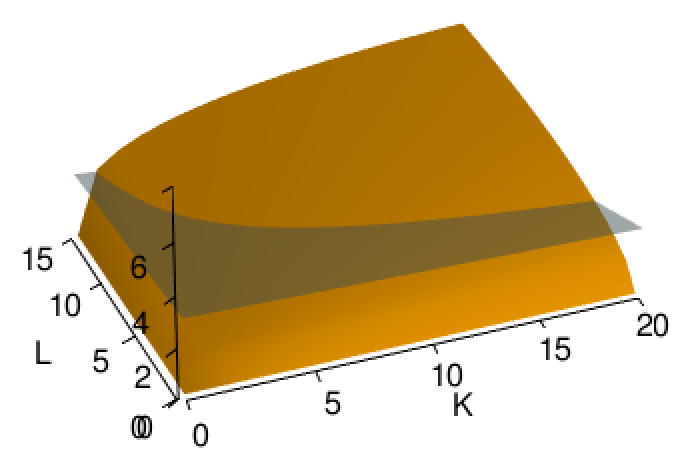
Amb R, segueix pas a pas les explicacions que trobaras aquí per obtenir coses com això:
Amb Wolfram Alpha, només introduir una expressió ja ens dona els gràfics: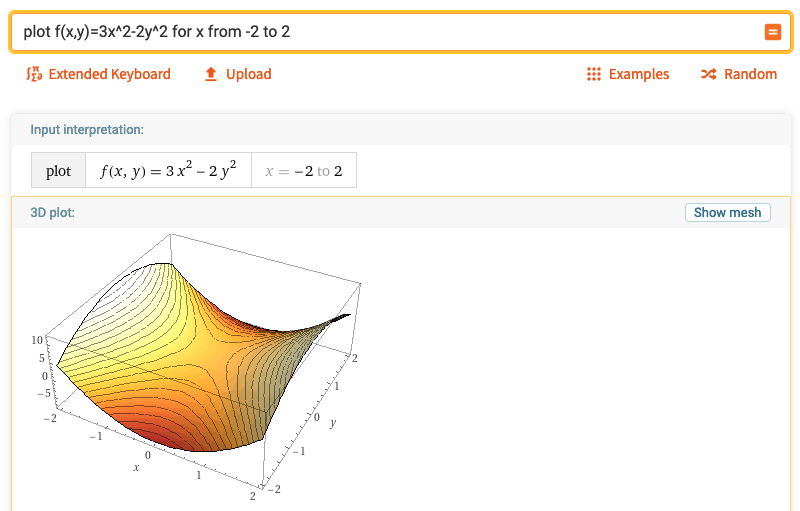
Un cop tens el gràfic pots triar si vols veure dibuixats sobre la superficie els isonivells o les linies de seccions
verticals/horitzontals.
Amb Geogebra les figures 3D són fàcils de produir, cal que obriu una finestra 3D:
I després entrar coses com això: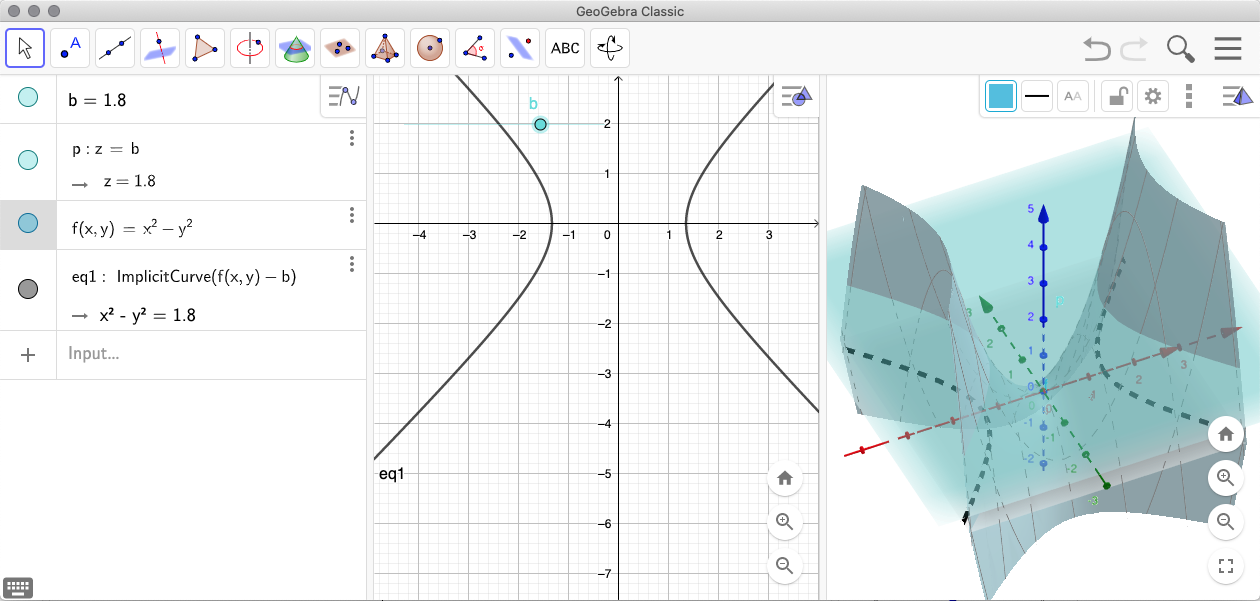
(Pots trobar-ho aquí. Si tens el Geogebra en Català, la instrucció serà CorbaImplicita)
Els gràfics d’isonivells no són tan fàcils de fer, però podeu trobar applets que ho facin.
En molts dels gràfics 3D que hem vist fins ara la superficie estàresseguida per unes linies que corresponen a valors fixos de x o
de y. Si fixem una de les variables, per exemple x = k per k constant, el que tenim és una funció d’una variable
z = z(y) = f(k,y) i la seva gràfica correspon a la secció vertical de la superficie z = f(x,y) segons el pla x = k. Mira’t i
reprodueix el que fem aquí amb R. Obtindras figures com aquesta: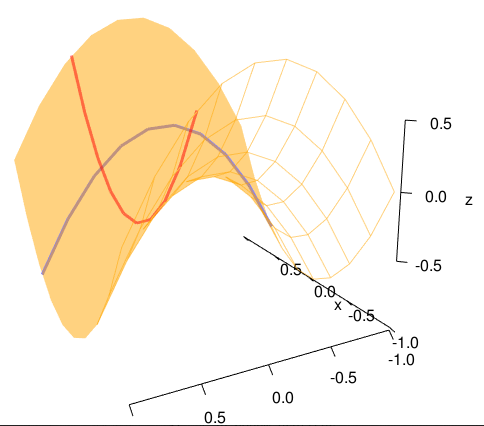
Obre l’enllaç de Geogebra. Veuràs alguna cosa com això: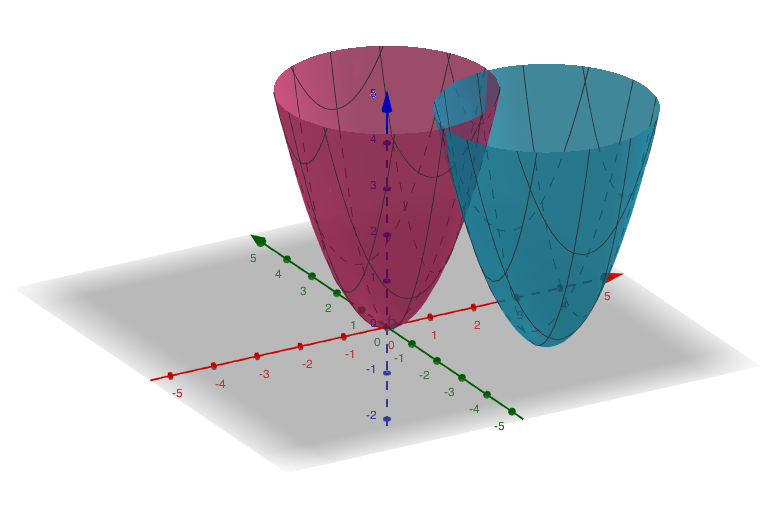
Prova de desplaçar els lliscants correponents a a i a b. Com expliques el què està passant?
Posa-hi ara la funció g(x,y) = (x - a)2 - (y - b)3. Quan a és positiu, cap a on es desplaça la gràfica? I quan b és positiu?.
Ara hi posem la funció g(x,y) = (ax)2 + (by)2. Posar al davant de la x un coeficient, per exemple a = 10 vol dir que enlloc de
mesurar les x en centímetres les passem a mesurar en milímetres, hem canviat l’escala. Pot veure l’efecte sobre el gràfic en
aquest applet de Geogebra.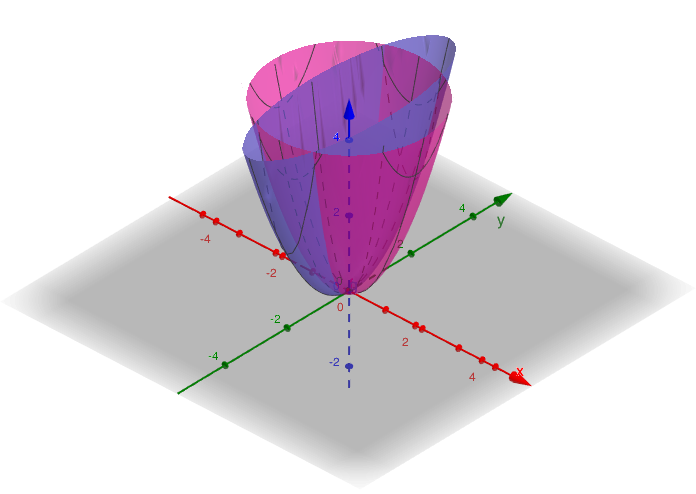
.
Ara pots contestar les següents preguntes:
QUIZZ
Si a la funció z = f(x,y) hi posem z = f(ax,y), el graf de la funció = es contrau en la direcció de l’eix x si a > 0 = es contrau
en la direcció de l’eix x si a > 1 = es contrau en la direcció de l’eix y si a < 1 == es contrau en la direcció de l’eix x si
a > 1
QUIZZ
i molts com aquest.
QUIZZ
Si tenim una corba d’isonivell donada per u(x,y) = uo, la gràfica de la corba d’isonivell u(x + 2,y) = u0
= estarà dues unitats més amunt
= estarà dues unitats més avall
= estarà dues unitats més a la dreta
== estarà dues unitats més a l’esquerra
= cap de les anteriors
QUIZZ
Si tenim una corba d’isonivell donada per u(x,y) = uo, la gràfica de la corba d’isonivell u(x,y) - 2 = u0
= estarà dues unitats més amunt
= estarà dues unitats més avall
= estarà dues unitats més a la dreta
= estarà dues unitats més a l’esquerra
== cap de les anteriors
Una activitat autònoma per alumnes espavilats, per matrícula?.
Hem vist que les derivades creuades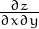 
i 
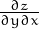són iguals. Sempre? No, per assegurar-ho cal que siguin continues. Pots
mirar a la Wikipedia Symmetry of second derivatives, informació sobre el tema. Pots resseguir els càlcul de l’exemple que
mostra que si no hi ha continuitat la simetria pot no complir-se.
A ma, o amb Geogebra o Wolfram Alpha o similar, defineix la funció f(,x,y) =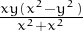 
. La funció no queda definida en el
(0,0), o sigui que hi afegim la definició f(0,0) = 0 amb la qual cosa la funció és continua.
Calcula ara les derivades respecte x, f′x(x,y), i respecte y, f′y(x,y). Per calcular la derivada segona f′′xy(0,0)
calcula f′x(0,y) i per calcular f′′yx(0,0) calcula f′y(x,0). Segons això, què obtens per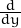 
f′x(0,y)? I què obtens
per 
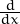f′y(x,0)? Són iguals? Calcula i grafica la segona derivada f′′xy(x,y) i observa què passa a prop del
(0,0.
Solució: en Geogebra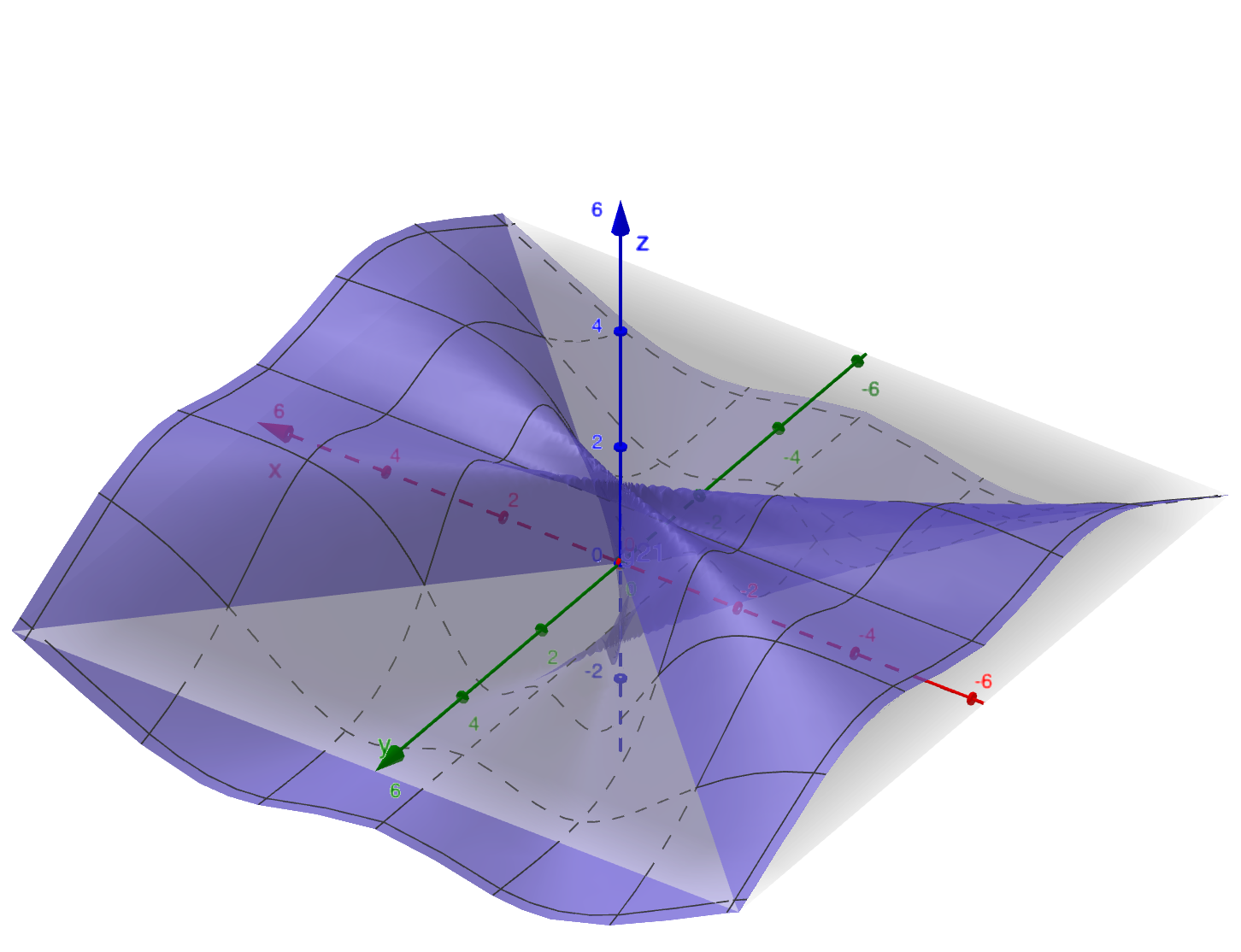
QUIZZ
Si tens el gràfic 3D d’una funció f(x,y) amb l’eix z en vertical com solem fer-ho. Una secció vertical segons un pla paral·lel al
pla ZX, correspon, per alguna constant k, a:
= una corba de nivell z = k
= una funció d’una variable z = f(k,y)
== una funció d’una variable z = f(x,k)
= Cap de les altres és veritable.
QUIZZ
Si dues corbes de nivell, de nivells respectius a i b corresponents a una funció f(x,y) tenen un punt en comú,
= Una de les dues ha der ser només un punt
= Això no pot donar-se mai
= Podem assegurar que a = b
= Les derivades parcials en aquell punt han de ser zero.