Índex

1 Objectius d’aprenentatge

• Matrius m × n com a espai vectorial de dimensió mn. La transposada, propietats
• Matrius quadrades. Determinants. Inversa. Propietats
• Matrius simètriques. Matrius diagonals
• Mínims quadrats, solució matricial.
• Formes quadràtiques, Matriu d’una forma quadràtica.

2 Prerequisits

El càlcul i propietats dels determinants es donaran per coneguts, se’n pot fer un breu repàs recopilatori, però no s’entrarà en demostracions que poden ser llargues i poc interessants.

3 Guia pel professor

Ja s’han vist algunes propietats de les matrius, bàsicament quadrades de dimensions dos o tres. Ara es tracta de generalitzar-ho en un plantejament més abstracte, on les propietats siguin més importants que els càlculs. Es farà veure que els càlculs amb matrius d’ordre 3 o superior es poden deixar en mans de software adequat (R, potser Excel, Wiris o WolframAlpha en cas simbòlic).

L’objectiu d’aquest tema, com l’anterior és acostumar l’estudiant a la manipulació simbòlica abstracta. També, naturalment, mostrar els conceptes i tècniques bàsiques del càlul matricial, però això es podrà complementar en els temes successius on s’aplicaran a la diagonalització i la classificació de les matrius de formes quadràtiques.

La classificació es farà segons valors propis. Es pot esmentar la regla de Descartes per saber el nombre de valors propis positius. No s’entrarà en signes de menors.

• L’espai _m,n com a espai vectorial. Subespais, base canònica.
• La operació transposició, propietats. El cas n × p de les matrius de dades multivariants.
• Matrius simètriques
• …

3.1 Presentació del tema

3.2 Materials bàsics

Les seccions 12.7, 12.8, 12.9 de S&H-MAE.

Cap 13.4 Quadratic forms and symmetric matrices del PembRau.

Per l’estimació per mínims quadrats, problema 13-4, pg 264 del PemRau.

Pot servir de referència (avançada) el capítol 1 de ÀLGEBRA LINEAL, ApuntsFMEBarcelona, Gener 2019, de Andreu Boix, Paolo Lammens, FME-UPC. https://apuntsfme.gitlab.io/pdfs/primer/algebra_lineal.pdf. Especialment per derivar-hi els estudiants interessats en aprofundir o en trobr demostracions que es deixen sense fer al curs.

4 Activitats autònomes

4.0.1 repassa R

Al primer trimestre, assignatura Anàlisi de dades, vas aprendre a fer anar R i RStudio. Repassa-ho i repassa també la sessió que aleshores vas seguir: R Programming: Matrices and Data Frames→3: R Programming→7: Matrices and Data Frames

4.0.2 Càlcul de matrius amb R

En aquesta activitat volem que aprenguis com efectuar càluls matricials amb R.

Has d’obrir RStudio (recordes les beceroles de R i RStudio? Si no, repassa-les aquí XXX.

Pots veure un resum ràpid de les funcions de R per treballar amb matrius a https://www.statmethods.net/advstats/matrix.html

Com a primer exemple, volem comprobar si la inversa de la transposada de A coincideix amb la transposada de la inversa per A = .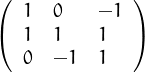

Per introduir la matriu fem servir la funció matrix que demana els elements de la matriu en una sola llista i després cal dir quantes files ha de tenir la matriu i si hem llistat els elements per files o no. La funció t calcula la transposada:

Per invertir una matriu fem servir la funció solve amb un únic argument (amb dos arguments serveix per resoldre sistemes lineals). Per tant t(solve(A)) donarà la transposada de la inversa, mentre que solve(t(A)) donarà la inversa de la transposada.

Amb això hem comprovat que en aquest cas la transposada de la inversa és el mateix que la inversa de la transposada, però no sabem si sempre es compleix això.

Vegem de demostrar que 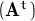^-1 = 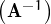^t, és a dir, comprovar que la matriu B = 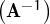^t és la inversa de A^t.
Demostració
Segons la definició de matriu inversa, cal comprovar que B ⋅A^t = A^t ⋅B = I, on I és la matriu identitat. I efectivament

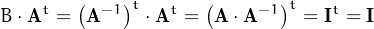
Ara omplim una matriu 5 × 5 amb els nombres del 1 al 25.

Pots calcular el determinant d’aquesta matriu amb det(C). Pots explicar perquè et dona zero? (Recorda que si substituim una columna o una fila per la diferència d’altres dos el determinant no canvia).

Aquí omplim una matriu amb nombres aleatoris. Farem servir el símbol adequat per la multiplicació de matrius en R: %*%. La suma i la multiplicació per nombres es fan amb els mateixos símbols que pels nombres: + i *.

Hem volgut comprovar la inversa de C2 i hem obtingut un resultat estrany, no sembla que el resultat. Pots explicar què ha passat?

Podem fer servir la funció round() per arrodonir el resultat a tres xifres decimals:

Hi ha molt d’altres software que permeten fer càlculs matricials, no els introduirem tots, podeu buscar i provar i triar el que més us agradi.

Per exemple, WolframAlpha pot fer càlculs simbòlic (és a dir, que involucrin lletres sense donar-les cap vaor numèric. Proveu-hi:
inverse {{6, a, b, 0}, {0, 1, -1, 3}, {1,1,-1,0}, {1, -1, 0, 0}}

Geogebra també us permet fer càlculs simbòlics amb la vista “CAS”. Podeu provar

També en Excel podeu càlculs matricials, per exemple =MMULT(A3:C5;A7:C9), =MINVERSA(A3:C5) o =MDETERM(A3:C5) us calcularà el producte de matrius, la inversa o el determinant.

Ara et toca a tu!

Quiz XXX

4.0.3 Exercicis PemRau 13.4

Els de la pàgina 262 de Cap 13.4 Quadratic forms and symmetric matrices del PembRau.

Solucions als exercicis del PemRau 13.4

Solucions als problemes del PemRau cap. 13

4.0.4 Les dades com a matriu. Càlcul de mitjanes, variàncies, estandardització

Per tractar amb dades multivariants és molt útil la notació i àlgebra matricials. Posem que tenim informació sobre n individus (per exemple empreses) i de cada individu tenim p variables numèriques X₁,…,X_p (per exemple X₁ podria ser el nombre de treballadors de l’empresa, X₂ el salari mitjà, etc). Habitualment es disposa la informació en una matriu X de dimensions n × p, és a dir cada fila correspon a un individu, i les columnes corresponen a les variables.

Llavors, si denotem 1_n = (1,…,1)′ el vector (vertical) que conté n uns, el producte X′1_n∕n = v_m serà el vector de les mitjanes de les variables, de [p × 1].

Si posem 1_nv′_m = 1_n1_n′X, tenim una matriu [n × p] amb columnes constants, la columna j conté n còpies de la mitjana de la variable j. Per tant X_c = X - 1_n1_n′X∕n és la matriu de dades centrades.

O bé, definim la matriu centradora: M = I - 1_n1_n′∕n, amb la qual cosa les dades centrades s’obtenen amb X_c = MX.

Per la traducció a R de tot això, farem servir les dades LifeCycleSavings que estan incloses a R.

Farem:

QUIZZ
Es poden plantejar preguntes per comprovar que ho fan

Es podria anar més enllà. Cal tenir present que molts d’ells han fet aquests conceptes a mates per socials.

• S = X_c′X_c∕(n - 1) matriu de variàncies/covariàncies.
• v_v = diag(S) vector de les variàncies.
• v_sd = v^1∕2 vector de desviacions estàndard. 1∕v_sd vector d’inverses de les desviacions estàndard.
• diag(1∕v_sd) és la matriu diagonal amb aquest vector a la diagonal.
• X_s = X_cdiag(1∕v_sd) matriu de dades estandarditzades.
• R = X_s′X_s∕(n - 1) matriu de correlacions.

4.0.5 Les formes quadràtiques com a funcions de dues variables

Es tracta de posar de manifest la relació de la matriu amb la forma quadràtica en el cas 2D, començant amb les matrius diagonals.

Gràfics de superficie, corbes de nivell, etc.

5 Llista d’exercicis

5.0.1 Càlculs amb R i amb altre software

Pots resoldre aquests exercicis amb R o amb el software que més t’agradi.

Introdueix la matriu C2 = 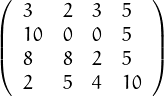. Calcula la seva inversa, el seu determinant. Comprova que el determinant de la inversa és igual a l’invers del determinant.

6 Suplements avançats

7 Exercicis per exàmens

1. A partir de les definicions, demostra que, donades matrius quadrades A,B, sempre es compleix
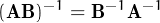
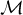2. A partir de les definicions, demostra que, donada una matriu A ∈ _m,n, la matriu producte A^tA és una matriu simètrica.
3. La descomposició en valors singulars (SVD) és una tècnica matricial molt útil en estadística i econometria per analitzar dades multivariants.
   Donada una matriu de dades estandarditzades X_s de dimensions n × p, posem X_n = X_s∕. La SVD dóna X_n = UDV′ on D és una matriu diagonal que conté n valors singulars a la diagonal.
   Quines són les dimensions de les matrius U i V?