El llenguatge de les matemàtiques
Projecte Math21, Departament Economia i Empresa, UPF
25 de març de 2021
Índex
Aquest és un document de treball INTERN, en fase de discussió i molt preliminar. No en feu difussió, sisplau.
1 Objectius d’aprenentatge
- Les beceroles del llenguatge formal
- Les connectives lògiques: conjunció, disjunció, negació, implicació
- Proposicions
- Tots o algún, els quantificadors
- El llenguatge dels conjunts
- Conjunts i elements
- Unió, intersecció, subconjunts
- El raonament matemàtic
- Definició, propietats, teoremes
- Demostracions
2 Prerequisits
No se’n presuposen.
3 Guia pel professor
3.1 Presentació del tema
Motivació: la necessitat del llenguatge formal per expressar idees de manera unívoca, per evitar ambigüitats.
En matemàtiques utilitzem lletres i altres símbols per representar no només nombres, també altres objectes, com funcions,
conjunts, o també proposicions, afirmacions que poden ser veritat o falses.
Caldrà fer el pont i el contrast entre el llenguatge formal i el llenguatge usual.
Començar amb exemples de demostracions errònies, arguments falaços, frases ambigües, etc
Empalmar amb demostracions senzilles tipus senar + senar és parell (IB-HL-An&App 5.1)
Introduir els símbols i els conceptes a través d’exemples i deixar-ho obert per les activitats autònomes.
3.2 Materials bàsics
SH-MAE:
- SH-MAE: 1.5 Algunos aspectos de lógica
- SH-MAE: 1.6 Demostración matemática
- SH-MAE: 1.7 Teoría de conjuntos
IB-HL-An&App
- 5. Proofs
- 5.1 Basic Laws and simple proofs
- 5.2 Direct proofs
4 Activitats autònomes
4.0.1 Conjunts
Pots llegir SH 1.7, o mirar-te aquests videos:
The Importance of Set Theory — Silvia Jonas
INTRODUCTION to SET THEORY (The Trev Tutor) 16 min.
[Discrete Mathematics] Set Operations Examples #2 (The Trev Tutor)
Set Operations & Venn Diagrams, part 1 127-1.20.a HCC MathHelp 9min.
Set Operations & Venn Diagrams, part 2 127-1.20.b 9 min.
Set Operations & Venn Diagrams, part 3 127-1.20.c 6min.
QUIZZ
Si A és el conjunt dels jugadors del Barça a la temporada 2019/20.
= Messi és un subconjunt de A
== Messi és un element de A
SET OPERATIONS - SET OPERATIONS - DISCRETE MATHEMATICS, Trev Tutor 7min.
4.0.2 Negació
Llegeix l’exemple 5.3 del IB-HL-An&App.
Respón aquest qüestionari.
La negació de la frase “A l’Anna li agrada la música pop” és
= A l’Anna no li agrada la música
= A l’Anna li agrada la música no-pop
= Si no l’hi agrada la música pop, no és l’Anna
= A l’Anna no li agrada la música pop
La negació de 2 < x < 4 és
= x > 4
= x ≤ 2
= x ≥ 4 i x ≤ 2
= x ≥ 4 ó x ≤ 2
…
4.0.3 Video sobre condicions suficients o necessàries
Necessary and Sufficient Conditions, Dr. Trefor Bazett (8min)
millor: Propositional Logic: Necessary and Sufficient Kevin deLaplante(5min)
QUIZZ
Marca les correctes:
Si diem que p implica q
= p és condició necessària per q
= p és condició suficient per q
= q és condició necessària per p
= q és condició suficient per p
QUIZZ
Marca les correctes:
= Ser un hipopòtam és CN per ser un animal
= Ser bomber és CS per ser persona
= Ser un cotxe és CN per ser una màquina
= Tenir 18 anys és CN per treure’s el carnet de conduir.
…
4.0.4 Implicació
Mira’t l’exemple 5.1, pag 217 del IB-AnAppr:

Fes ara aquests exercicis:

Solució: aquí
Llegeix 1.5 del SH.
(Aquests quizzes són el problema 3 de les pàgines anteriors)
QUIZZ
Sigui A(x) : 2x + 5 > 13 i B(x) : x ≥ 0. Tria la correcta:
== A(x) és CN per B(x)
=A(x) és CS, per B(x)
= A(x) és CN i CS per B(x)?
QUIZZ
Igual pregunta amb A(x) : x ≥ 50 i B(x) : x ≥ 0.
QUIZZ
Igual pregunta amb A(x) : x ≥ 0 i B(x) : x ≥ 4.
QUIZZ
En el llenguatge de la teoria de conjunts, A ⇒ B equival a
== A ⊂ B.
= B ⊂ A
= A ∈ B
= A ∩ B
4.0.5 Video sobre implicació i negació
Khan Academy: Conditional statements and deductive reasoning (4min)
En aquest video t’han explicat que p ⇒ q és equivalent a ⌝q ⇒⌝p.
Després de veure el video, se’ls plantegen exercisis tipus La proposició “Si mires la tele perds el temps” és
equivalent a la proposició “Si aprofites el temps, no mires la tele” o és equivalent a “Si no mires la tele, perds el
temps”
4.0.6 Video sobre proposicions condicionals i veritat
Khan Academy: Understanding Logical Statements 1 (4min)
QUIZZ
En una proposició condicional hi ha dos termes: l’antecedent i el conseqüent. En la proposició “Si les vaques volen, jo sóc
Buda”,
= no hi ha antecedent perquè la proposició és falsa
= l’antecedent és “jo sóc Buda”
= L’antecedent ’es “Si les vaques volen” = el conseqüent és “jo no sóc Buda”
QUIZZ
la proposició “Si les vaques volen, jo sóc Buda”,
= és falsa perquè les vaques no volen
= és falsa perquè jo no sóc Buda
=és falsa si la diu Buda
= és veritable
Per reforçar la idea que una implicació és falsa només quan l’antecedent ho és i el consequent no:
QUIZZ
Tenim una llista de persones (amb inicials o amb noms propis) i la seva categoria professional a l’empresa (directiu=D /
treballador=T, o desconegut=X).
A: La Maria és X
B: S. és D
C: En Joan és X
D: L. és T
Si volem demostrar que “Totes les dones són treballadores”, quines dades de la llista hem d’aclarir com a
mínim:
= A,B,C i D (Resposta incorrecta: No importa saber si en Joan és o no D)
= C i D (Resposta incorrecta: No importa saber si en Joan és o no D, tampoc cal saber si L és dona o home)
= No es pot saber ni aclarint totes les dades (Resposta incorrecta, només cal saber que S. no és dona)
== la B (Resposta correcta)
I variants... amb “Cap dona és directiva”, etc...
4.0.7 Conjuncions, disjunctions i negació
QUIZZ
La negació de “Plou i fa sol” és
= No plou i no fa sol
= Ni plou ni fa sol
== No plou o no fa sol
= Plou però no fa sol
4.0.8 Demostracions senzilles
Una demostració o prova matemàtica és una cadena de raonaments en la que cada afirmació és condició necessària de
l’anterior. El punt de partida d’una demostració és o bé les deficnicions dels termes que intervenen, o alguna propietat que ja
es coneix.
Llegeix la pàgina 204-205 del IB-HL-An&App. Has entés la demostració de l’exemple 5.1? Comprovem-ho. Hauries de ser
capaç d’escriure la demostració que la suma d’un nombre senar i un parell és senar. Porta-la al seminari per si te la
demanen.
Idem per: El producte de dos nombres senars és senar.
Idem per: Si n ≥ 2, n! + 2 és parell. (Recorda que n! es defineix com el producte dels nombres 1,2,…,n.
És cert que la suma de tres enters consecutius és divisible per 3? És certa la afirmació per quatre? La teva resposta ha de ser o
una prova o un contraexemple.
Molt bé, però alerta amb les demostracions, TOTS els passos han de ser correctes, si no, es pot arribar a qualsevol conclusió.
Vegeu si no aquest video: Proof that 1 = 2, by John Hush
4.0.9 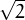 és irracional
és irracional
Què vol dir irracional? Mira’t el video (8m) de la Kahn Academy: https://www.youtube.com/watch?v=mX91_3GQqLY
Que perquè això és important? Mira’t aquest altre (5m) de Hotel Infinity: https://www.youtube.com/watch?v=nT4geKdKVfw
Has entés la demostració?
Quiz: Què vol dir demostrar P per contradicció?
= Vol dir que hem de trobar dues afirmacions contradictòries a partir de P
= Vol dir que el que volem demostrar és contradictori
= Vol dir que a partir de la negació de P hem de demostrar-ho
= Vol dir que partint de la negació de P hem de arribar a una contradicció.
Pots demostrar que 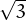 és irracional? Escriu la demostració i porta-la a classe per si te la demanen.
és irracional? Escriu la demostració i porta-la a classe per si te la demanen.
5 Llista d’exercicis
5.0.1 Petites demostracions
- Demostra que si
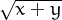 =
= 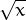 +
+ 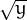 , llavors un dels dos x o y ha de ser zero.
, llavors un dels dos x o y ha de ser zero.
- Demostra que la suma de 5 nombres enters consecutius és divisible per 5.
- Demostra que per n ∈ Z, 5n + 3 és parell si 7n - 2 és senar.
- Demostra que A ∩ B ⊂ B per qualsevol conjunts A,B.
- Demostra que si A,B són conjunts qualssevol, A ⊂ A ∪ B.
- Demostra que si A,B són conjunts qualssevol, A ∩ B ⊂ A ∪ B.
- Si A és l’interval (0,2) de la recta real, quin és el conjunt Ac ∩(1,10)?
5.0.2 Eficiència Pareto
En el llibre de text de Introducció a la Microeconomia que esteu estudiant trobem, a 5.8.1 La curva de eficiencia de Pareto la
següent definició: Una asignación factible es eficiente en términos de Pareto si no existe una asignación dominante en
términos de Pareto: es decir, nadie puede mejorar sin empeorar la situación de otro.
Llegeix altre cop el capítol si no tens clar què vol dir la eficiència en termes Pareto.
Posem el cas que més de dos agents intervenen.
Digues si les següents definicions alternatives serien o no correctes:
= Una asignació és Pareto eficient si en canviar a una altra assignació algun agent millora més que els altres.
SI/NO
= Una asignació és Pareto eficient si en canviar a una altra assignació ningú millora SI/NO
= Una asignació és Pareto eficient si en canviar a una altra assignació només un millora i els altres no SI/NO
Posem el cas que hi ha dos agents A1,A2 i definim les proposicions Pi :Ai millora. Suposem que estem en una situació Pareto
eficient,
== Si P1, llavors ⌝P2 SI/NO
Llavors: (digues si són o no veritat les següents afirmacions)
== Si P1, llavors ⌝P2 SI/NO
= Si ⌝P1 llavors P2 SI/NO
== Si P1 ∧ P2 llavors 0 = 1 SI/NO
== És possible que P1 ∨ P2 SI/NO
Posem ara que estem en una situació no eficient en termes de Pareto i canviem a una nova assignació. Llavors: (digues si són
o no veritat les següents afirmacions)
= Si P1, llavors ⌝P2 SI/NO
== És possible que P1 ∨ P2 SI/NO
= Si ⌝P1 llavors P2 SI/NO
6 Suplements avançats
IB-HL-An&App
- 5. Proofs
- 5.3 Indirect proofs
- 5.4 Mathematical induction
Els qüestionaris del MathCenter: Boolean algebra http://www.mathcentre.ac.uk:8081/mathseg/
Colecció de videos molt completa sobre Set Theory: The Trev Tutor
7 Exercicis per exàmens
- Demostra que
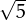 és irracional. Caldrà fer servir que si a2 és múltiple de 5, a també ho ha de ser.
és irracional. Caldrà fer servir que si a2 és múltiple de 5, a també ho ha de ser.
- Demostra que la suma de sis enters consecutius és divisible per tres.
- Si A = (0,10) i B = (-5,5), quin interval correspon a Ac ∩ B
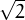 és irracional
és irracional


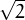 és irracional
és irracional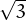 és irracional? Escriu la demostració i porta-la a classe per si te la demanen.
és irracional? Escriu la demostració i porta-la a classe per si te la demanen.
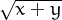
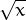
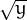 , llavors un dels dos
, llavors un dels dos 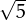 és irracional. Caldrà fer servir que si
és irracional. Caldrà fer servir que si