
(Enllaç a aquest document en html)
(Enllaç a la versió pdf d’aquest document)
(Enllaç a la font LaTeX)
(Enllaç als fitxers de les figures)
(Enllaç al fitxer de definicions latex)
Aquest document és una resposta a la petició de la coordinació de Matemàtiques d’orientar com el nou llibre de text pot cobrir el que es fa actualment a Matemàtiques I. També es complementa amb la proposta de Clickers o qüestionaris de conceptes ràpids.
S’inclou tanbé una proposta completa del que podria ser una nova primera setmana dedicada a una petita introducció al llenguatge formal de les matemàtiques.
Queda per tant per decidir la configuració final del temari del curs de Matemàtiques I.
Per cada guia assenyalo els exercicis del llibre Pemb-RAU que pertoquen. Estan disponibles al web del llibre les solucions als exercicis, i als problemes.
Amb la doble intenció de fer les classes de teoria més interactives i d’aprofondir en els aspectes més conceptuals dels temes tractats es proposa que es destini part del temps de les classes a la formulació i discusió de preguntes de resposta múltiple en una seqüència com ara la següent.
Hi ha un llibre que pot ser interessant: Teaching Mathematics with Classroom Voting With and Without Clickers. Aquí tenim l’index.
Moltes de les preguntes proposades a continuació provenen de la colecció de la Cornell U. Aquests fan servir un codi:
Un altre recurs interessant: http://mathquest.carroll.edu/ La seva colecció completa. Més avall fem referència a algunes parts.
Moltes altres són possibles, però la idea és que no siguin preguntes que requereixin gaire càlculs sino més aviat la comprensió i reflexió sobre els temes que s’han explicat a classe o que se suposa que els estudiants han revistat pre-classe.
Es tracta de fer una lleu introducció al llenguatge formal, limitat a l’àlgebra de conjunts i la de Boole elemental. Posem davant els conjunts perquè probablement els són més familiars i els poden ajudar a entrar en el més abstracta de la lògica formal, que tractem només somerament, sense entrar en taules de veritat, demostracions, etc. que poden ser objecte de tractament a mates II o III.
El material per aquest tema es troba a
(en html)
(versió pdf )
(font LaTeX)
(Enllaç als fitxers de les figures)
(Enllaç al fitxer de definicions latex)
Convindria aprofitar aquest tema per esmentar que les funcions poden ser de una o de més vairables, simplement algun exemple. També la idea de funció composta es pot introduir ja.
Vegeu els capítols 3.3 i 3.4 del Pem-Rau:
Exercicis 3.3.1, 3.3.2, 3.3.3, 3.3.5 
Exercicis 3.4.1, 3.4.2
i problemes 3-1, 3-2, 3-3, 3-4

Questions senzilles sobre el concepte de funció, domini, recorregut, es poden trobar a Classroom Voting Questions: Precalculus. Functions and Change
Per exemple
Which of the following functions has its domain identical with its range?
(a) f(x) = x2
(b) g(x) = 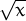
(c) h(x) = x4
(d) i(x) = |x|
Potser aquest ema i l’anterior es podrien fondre, no?
Questions senzilles sobre el concepte de funció, domini, recorregut, es poden trobar a Classroom Voting Questions: Precalculus. Functions and Change
Per exemple
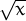
O de Cornell:
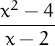 and g(x) = x + 2, then we can say the functions f and g are equal.
and g(x) = x + 2, then we can say the functions f and g are equal.
Answer: False. Note that even if the two functions have the same rule, they are defined on different domains, i.e., f is not defined at 2.
No entenc molt bé perquè es tracten aquí les funcions exponencials. Em semblaria més coherent tractar lineals/potencials.
El tractament de les quadràtiques jo el faria basat en “quadrar l’expressió”, és a dir transformar-la en la forma y = a(x - p)2 + q
El 4.3 va sobre potències, exponents i funcions potencials.
El llibre tracta les funcions exponencials després de la derivació i juntament amb els logaritmes. Llavors entra en el tema del creixement amb totes les eines a punt. Té sentit.
Si es tractés amb potències i funcions potencials, exercicis 4.3.1 a 4.3.9: 
Moltes questions a: Classroom Voting Questions: Precalculus. Lines and Parabolas
I també a Classroom Voting Questions: Precalculus. Exponential Functions
El tema del desplaçament de gràfiques crec que s’hauria de contextualitzar més, no hi veig sentit si es planteja com unes regles que s’aprenen de memòria per respondre preguntes tipus. Si de cas, s’ha de lligar amb exemples on hi hagi canvis d’origen, canvis d’escala, etc.
Del llibre:
Tindria sentit imtropduir aqui la programació lineal amb resolució gràfica?
Sobre desiguatats lineals, 2.2.1 a 2.2.3: 
En el problema PR 3-2 es tracta el tema de canvi de variable per tractar el desplaçament.
Aquest tema el trobo desproporcionadament complex i difícil, sobretot si el comparo amb els primers del curs. Crec que tractar la continuïtat i els límits cap a ±∞ sense haver parlat abans de limits...
Potser algunes coses de polinomis s’haurien de moure als T2 o T3.
En el llibre Pem-Rau:
En el llibre, el capítol comença amb succession, series i progressions geomètriques en economia, temes que aquí no tractem.
Pel que fa a límits, fa una definició “verbal” i després també entra en ϵ∕δ. Dona les regles aritmètiques dels límits, i posposa les demostracions aun capítol 31 on fa l’anàlisi amb rigor. Tracta de passada els polinomis com a exemple de funcions continues, tracta breument la indeterminació 0∕0 i els límits laterals. Després tracta la continuïtat. I el T. Valor Intermedi, el de Bolzano no l’esmenta.
En aquest primer test, si es creu que els estudiants no tenen clara la distribució dels irracionals a la recta real, es podria canviar la definició: x2 o -x2 segons si la tercera xifra de l’expressió decimal de x és o no zero.
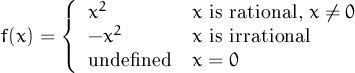
Then
Answer: (c). Students should be encouraged to draw the graph and discuss.
Answer: True. Students must consider the difference of two functions: f(t) = height(t) - weight(t), functions of time. At birth, f(birth) > 0 and right now, f(now) < 0, hence by IVT f(T) = 0, where T is some time in the past. It is important to stress that this technique of looking at the difference of two functions is recurrent in calculus.
Answer: False. As x increases to 100, f(x) = 1∕x gets closer and closer to 0, gets closer and closer to 1∕1000, but not as close as to 1∕100. The question points out the weakness of the statement ”f(x) gets closer to L as x → a, and therefore limx→af(x) = L”.
If f(x) is a polynomial, then f(x) is continuous.
Which of the following is also true?
Answer: (a). This may seem like an easy logic question, but students tend to have difficulties; it might be a good time to review some logic. This question prepares students for reasoning that even if differentiability implies continuity, continuity does not imply differentiability. Ask for examples of functions that are continuous, but not polynomials.
Answer: True. Students must consider the difference of two functions: f(t) = height(t) - weight(t), functions of time. At birth, f(birth) > 0 and right now, f(now) < 0, hence by IVT f(T) = 0, where T is some time in the past. It is important to stress that this technique of looking at the difference of two functions is recurrent in calculus.
Answer: True. This problem is not a direct application of IVT, plugging in 0 and 2, we get positive numbers, so the student must choose some other number in [0,2] to test. Choosing 0 and 1, or 1 and 2, IVT immediately applies.
El Perm-Rau tracta les exponencials despr´s d’haver vist la derivada. Té sentit perquè el més interessant de la funció exponencial és el creixement. Es pot donar per suposat que ja saben alguna cosa de derivades i fer-ho així?
Classroom Voting Questions: Precalculus: Powers, Polynomials, and Rational Functions
Exercicis 6.4 i Problemes capítol 6: 

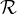 . Prepara’t per
raonar si és certa perquè, i si és falsa a mostrar un contraexemple.
. Prepara’t per
raonar si és certa perquè, i si és falsa a mostrar un contraexemple.
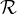 .
.
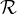 .
.
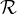 .
.
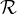 .
.
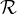 , no pot tenir cap punt estacionari.
, no pot tenir cap punt estacionari.
N’hi ha una àmplia col·lecció a el projecte Carrol U., però aquí en recollim alguns de la Cornell:
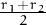
Answer: (d). This is a straightforward application of the definition of average rate of change. Once we get (c) as an answer, (a) and (b) follow:
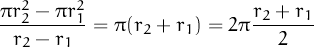
Answer: (a). Instructors should encourage the use of the limit definition of derivative; f′(0) = 0
Answer: (b). If f is differentiable at a, it must be continuous at a, and therefore the limit equals f(a). Many students will like answers (a) and (d).
Answer (b). Once the students realize that f′(x) is the speed of the train after x hours, most of them will give the right answer.
Answer: (a). Students will know that I holds. They might have questions about II and not be quite sure about III.
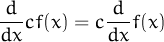
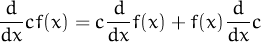
Answer: True. Some students will be unable to recognize that we get the same result. Remind them that the derivative of a constant function is zero.
Answer: (c). Even though students may have memorized the Chain Rule formula, some may not be able to apply it to this type of problem.
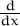 ln(π) =
ln(π) = 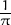 .
.
Answer: False. Students must observe that ln(π) is a constant, and thus 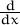 ln(π) = 0.
ln(π) = 0.
La regla de la cadena la he inclós en l’anterior secció, la derivada implícita el llibre la tracta molt més endavant, amb el teormea de la funció implícita. Però està bé tractar-ho aquí, de fet s’hauria d’aprofitar per enllaçcar amb el que veuen a Inroducció a Micro, isoquantes i demés. Això ho tracta bé el llibre
De tipus més calculets, poc interessants: Classroom Voting Questions: Calculus I: 3.7 Implicit Differentiation
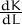 o bé respecte L,
considerant que K depén de L i obtindrem
o bé respecte L,
considerant que K depén de L i obtindrem 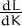 . Aleshores es compleix:
. Aleshores es compleix:
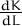 = 1∕
= 1∕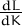
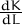 = -1∕
= -1∕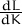
4,5 i 6, 9, 10 del capítol
Answer: (c). Most students will be able to get a correct formula for the linearization of ex at 0, L(x) = 1 + x, but a good number will have difficulties knowing how to use this information to get an approximation for e.5.
Answer: (c). If f is the stock price, and we found out that f′ is increasing, this does not lead to any conclusion about the monotonicity of f.
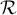 , i un punt x0 ∈
, i un punt x0 ∈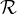 , digues quines són certes o falses
, digues quines són certes o falses
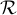 , i un punt x0 ∈
, i un punt x0 ∈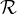 , digues quines són certes o falses
, digues quines són certes o falses
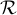 , f′′(x0) no pot ser zero.
, f′′(x0) no pot ser zero.
True or False. f might have an absolute maximum at x = a.
Be prepared to give a counterexample or justify your answer.
Answer: True. Consider a function with a cusp at x = a and f(a) = 1, which remains positive, and decreases to a horizontal asymptote at y = 0 .
Answer: False. Encourage the students to think of the different ways in which this would fail -i.e. the endpoints, points where the derivative does not exist.
Answer: (a). Students should think about the differences between local and absolute extrema. Ask students to draw pictures of functions satisfying f′(a) > 0, with a being the left endpoint, and then a being the right endpoint.
Answer: (a). (c) omits the possibility that the max or min could occur at a point on the graph where f′(x) does not exist (such as a cusp), and (b) is false by the Extreme Value Theorem.
The above statement is:
Answer: (a). This problem emphasizes one important application of the EVT which is at the same time a very geometric result; that we can put a continuous function on a closed interval inside a box! On a closed interval, m ≤ f(x) ≤ M, so if we take A = max{|m|,|M|}, then on this closed interval, f fits in this sort of box. This idea will ultimately show up in finding bounds for integrals, so it would be great to introduce this idea at this point.
True or False: You can find the position of the object at any time t.
Answer: False. The goal is to test whether students understand that they need one initial condition for each antiderivative they have to find.
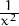 , and F(x) be an antiderivative of f with the property F(1) = 1. True or False. F(-1) = 3.
, and F(x) be an antiderivative of f with the property F(1) = 1. True or False. F(-1) = 3.
Answer: False. f(x) is not continuous at 0 ! This problem may help them remember the continuity condition in finding antiderivatives. Students are almost surely going to answer true, and the answer will surprise them.
Answer: (b). This follows from the definition of antiderivative. This kind of problem makes the connection between antiderivatives and derivatives.
Answer: True. This is an easy check based on the text reading.
Answer: False. Students should differentiate an antiderivative of f times an antiderivative of g, to see that they will not get fg back.
Answer: True. This problem helps students to use the summation notation to represent physical quantities. It also gets the students to distinguish between the estimating procedure of a Riemann Sum versus cases in which we can have an exact value.
Answer: (d). Students often hold onto the idea that the midpoint estimate is the best. With this example the instructor can point out that there are cases in which it does not work as well as some of the other height choices. A specific function which has a long thin spike at the midpoint is a good counterexample.
Answer: (c). This is a quick application of the area approximations in this section. Once students understand the set up of the problem, the right answer should follow immediately from the text reading.
If f is continuous on the interval [a,b], then:
Answer: (a). This problem attempts to clarify most of the misconceptions that students have about definite integrals, and to help them move away from the idea that they always represent the area under a curve.
Answer: (a). This question might also help students see the definite integral as total change rather than the standard area interpretation. At the same time it differentiates it from averages.
The following 2 problems to be used in a sequence:
Answer: True. See below
Answer: False. As students often get confused in the mechanics of the process of going back and forth between functions, their derivatives and antiderivatives, a discussion using the above problem can help them clarify their misunderstandings.
Answer: (c). f is the derivative of G, thus f > 0 implies G′ > 0, and therefore G is increasing. This is to demonstrate to students that they can apply the Increasing/Decreasing Test outside the context of problems like those in Chapter 4. Note that here we are just referring to the antiderivative of f. (a) may be a popular answer since we think of an integral of a positive function as ”adding”positive small pieces. But the choice between (a) or (b) for a particular antiderivative G, depends on the constant.
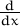
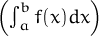 = f(x).
= f(x).
Answer: False. Students often do not realize that definite integrals evaluated at constant endpoints a and b are constant, and in order to apply the FTC one must have one at least one of the endpoints as a variable. Note that if a and/or b were defined as functions of x, then the answer would be True.
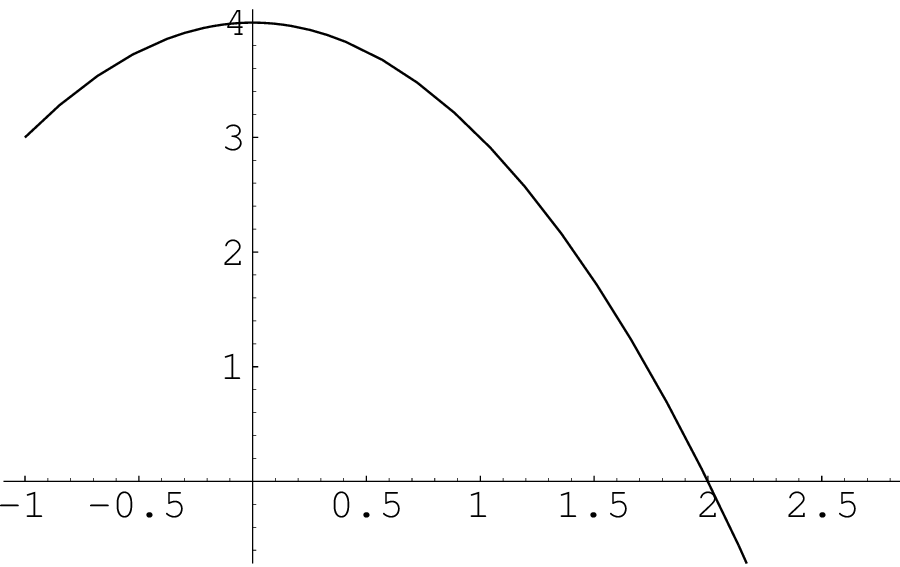
Let g(x) = ∫ 0xf(t)dt. Then for 0 < x < 2, g(x) is
Answer: (b). This problem can help students realize that an integral of this form is a specific function (not a general antiderivative), and the integrand is its derivative. Students can induce information about the concavity of g just like they normally would with any other function, only that this time they have to look at f.

Let g(x) = ∫ 0xf(t)dt. Then
Answer: (b). g(0) = 0, g′(0) = f(0) = 4, and g′(2) = f(2) = 0.
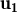 ,
,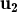 ,
,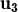 vectors no nuls de
vectors no nuls de 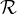 3 i sabem que
3 i sabem que 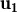 és combinació lineal dels altres dos amb
és combinació lineal dels altres dos amb 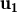 = λ
= λ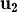 + μ
+ μ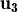 ,
llavors
,
llavors
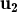 és CL dels altres dos.
és CL dels altres dos.
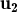 és CL dels altres dos si λ≠0
és CL dels altres dos si λ≠0
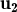 és CL dels altres dos si λ i μ són diferents de zero.
és CL dels altres dos si λ i μ són diferents de zero.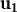 ,
,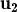 ,
,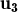 ,
,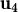 vectors no nuls de
vectors no nuls de 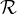 3 i sabem que
3 i sabem que 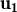 és combinació lineal dels altres tres amb
és combinació lineal dels altres tres amb
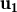 = λ2
= λ2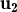 + λ3
+ λ3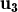 + λ4
+ λ4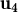 , llavors
, llavors
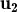 és CL dels altres tres
és CL dels altres tres
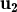 és CL dels altres tres si λ2≠0
és CL dels altres tres si λ2≠0
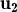 és CL dels altres tres si totes les λ són diferents de zero.
és CL dels altres tres si totes les λ són diferents de zero.
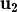 no sigui CL dels altres tres.
no sigui CL dels altres tres.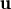 +
+ 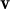 ) és igual a
) és igual a
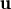 +
+ 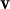 ) + μ)(
) + μ)(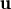 +
+ 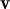 )
)
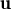 + (λ + μ)
+ (λ + μ)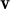
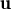 + λ
+ λ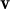 + μ
+ μ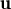 + μ
+ μ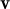
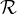 3?
3?
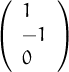 ,
,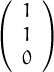 ,
,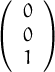
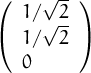 ,
,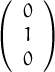 ,
,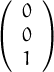
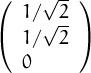 ,
,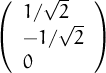
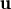 ,
,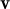 vector ortonormals de
vector ortonormals de 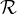 3, llavors, ||
3, llavors, ||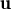 +
+ 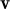 || és
|| és
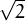
Unes notes breus sobre l’ús en R en versió html o en versió pdf
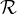 és
és
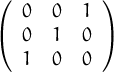
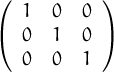
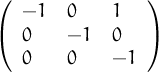
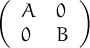
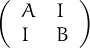
Unes notes breus sobre l’ús en R en versió html o en versió pdf
Resposta: És zero: si restem la fila 2 menys la fila 1 tenim tots els elements iguals a n, la posem enlloc de la primera. Fem el mateix a la segona: fila 3- fila 2, també tots iguals a n. Queden dues files iguals, el determinant és zero.
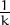 |A|
|A|
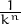 |A|
|A|
Unes notes breus sobre l’ús en R en versió html o en versió pdf
Resposta: |A| = |AT | i |A ⋅ AT | = |I| = 1, per tant |A|2 = 1.
Tria la correcta: